معادلات خطی همگن و ناهمگن

در آموزش گذشته، باروش حل معادلات دیفرانسیل مرتبه دوم آشنا شدیم. در این آموزش معادلات دیفرانسیل لینوم، قصد داریم به سراغ یادگیری معادله دیفرانسیل جداشدنی و معادله دیفرانسیل همگن برویم.

فرم کلی این معادلات به صورت زیر است:

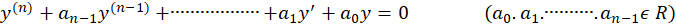
و معادله مفسر آن‌ها نیز به شکل زیر است:

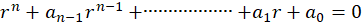
 توجه کنید که درمعادله دیفرانسیل فوق منظور از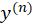  مشتق مرتبه 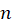ام است.

روش حل معادلات خطی و همگن از مرتبه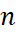 با ضرایب ثابت

برای حل این معادلات نیز با حالات مختلفی روبرو خواهیم شد که هر کدام از آن‌ها به شیوه خاص خود حل می‌شوند.در ادامه به بررسی هر یک از این موارد خواهیم پرداخت.

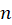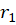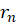1-معادله مفسر دارای ریشه ی حقیقی و متمایز تا است ، در این صورت جواب عمومی معادله برابر است با:

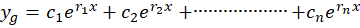
2-معادله دارای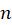 ریشه ی حقیقی است که 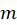تای آن تکراری است:

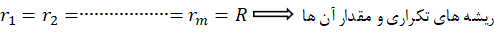
و جواب عمومی این معادله به شکل زیر است:

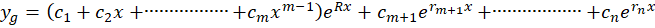
در واقع باید گفت این جواب ترکیب دو جواب مختلف است.قسمت دوم جواب که برای ریشه‌های متمایز است در واقع همان حالت اول این گونه معادلات را بیان می‌کند.در مورد قسمت دوم هم باید گفت که در حالت کلی اگر معادله دارای ریشه تکراری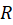 از مرتبه 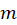باشد آن گاه جواب عمومی معادله برابر با عبار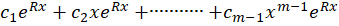ت است.

3-اگر معادله دارای دو ریشه ی مختلط غیرتکراری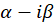 و باشد ،جواب عمومی معادله به شکل زیر است:

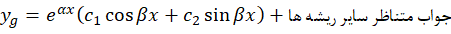
4-اگر معادله دارای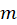 ریشه مختلط تکراری به شکل 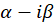یا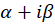 باشد فرم کلی جواب عمومی به صورت زیر است:

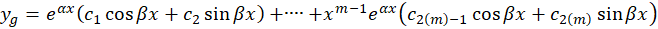
مثال) معادله 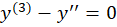 را حل کنید.

ابتدامعادله مشخصه را نوشته و ریشه‌های آن را به‌دست می‌آوریم:

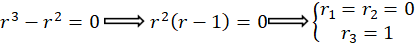
با توجه به ریشه‌ها متوجه می‌شویم با حالت دوم روبرو هستیم پس داریم:

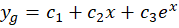
مثال) معادله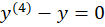 را حل کنید.

ابتدا معادله مشخصه را نوشته و ریشه‌های آن را به‌دست می‌آوریم:

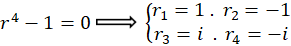
با توجه به ریشه‌ها با حالت سوم روبرو هستیم و داریم:

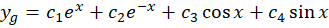
مثال) معادله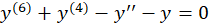 را حل کنید.

ابتدا معادله مشخصه را نوشته و ریشه‌های آن را به‌دست می‌آوریم:

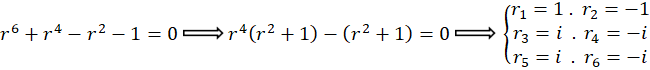
با توجه به ریشه‌ها با حالت چهارم روبرو هستیم پس داریم:

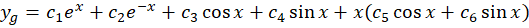
معادلات خطی ناهمگن مرتبه دوم و بالاتر

معادلات خطی ناهمگن مرتبه دوم و بالاتر هم می‌توانند دارای ضرایب ثابت باشند و هم ضرایب غیرثابت. ما در ابتدا معادلات دارای ضرایب غیرثابت و روش حل آن‌ها را بررسی می‌کنیم و سپس به سراغ معادلات دارای ضرایب ثابت می‌رویم.

معادلات خطی ناهمگن مرتبه دوم و بالاتر دارای ضرایب غیرثابت

فرم کلی این معادلات به صورت زیر است:

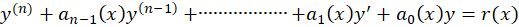
روش حل معادلات خطی ناهمگن مرتبه دوم و بالاتر دارای ضرایب غیرثابت

در ابتدا به بررسی حالت خاص مرتبه دوم این معادله می‌پردازیم و در نهایت یک روش کلی برای حل این دسته از معادلات با هر مرتبه‌ای ارائه می‌کنیم.

معادله فوق در حالت مرتبه دوم به شکل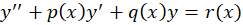 می‌باشد.برای حل این معادله کافیست یکجواب خصوصی از آن و جواب عمومی آن در حالت همگن شده را داشته‌باشیم زیرا:

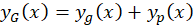
که در این عبارت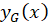 و جواب عمومی معادله فوق، 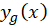جواب عمومی آن در حالت همگن شده و 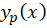جواب خصوصی آن است.

در مورد به‌دست آوردن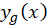 پیش از این صحبت کرده‌ایم و مقدار آن را برابر با 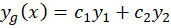فرض می‌کنیم.پس تنها مقدار 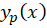مورد نیاز است که آن را به شکل 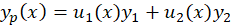در نظر می‌گیریم.مقدار 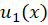و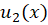 از رابطه‌های زیر به‌دست می‌آیند:

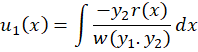
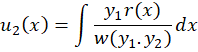
پس در نهایتجواب عمومی معادله از رابطه زیر به‌دست می‌آید:

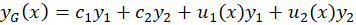
حال می‌خواهیم بررسی کنیم که اگر معادله از مرتبه می‌بود روابط فوق به چه شکلی در می‌آمد. برای حلمعادلات خطی ناهمگن مرتبه 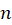 باز هم از رابطه 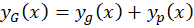استفاده می‌کنیم فقط با این تفاوت که 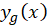برابر است با:

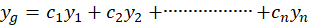
و همچنین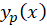 نیز برابر است با:

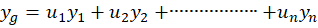
برای بدست آوردن 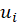 ها باید بدانیم  یک رابطه کلی وجود دارد که به شکل زیر است:

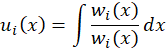
و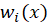 همان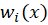 است که ستون 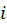ام ماتریس آن برابر با است

مثال) معادله 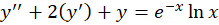 را حل کنید.

ابتدا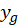 که جواب عمومی معادله همگن شده است را به‌دست می‌آوریم:

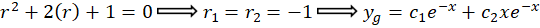
پس با توجه به این که 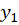 و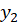 در رابطه بالا مشخص شد داریم:

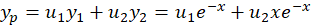
حال بایدرونسکین دو تابع را حساب کنیم:

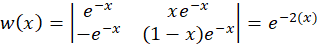
برای به‌دست آوردن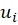 ها باید 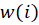ها را به‌دست آوریم:

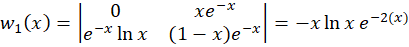
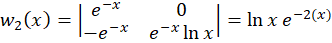
اکنون می توانیم مقدار 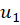 و 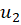 را مشخص کنیم:

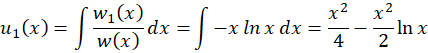
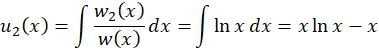
پس برابر است با:

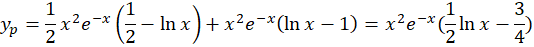
و نهایتا جواب عمومی معادله برابر است با:

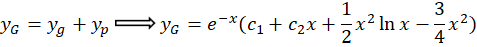
توجه کنید که شما در محاسبهرونسکین همیشه با دترمینان ماتریس‌های دو روبرو نخواهید شد و ماتریس می‌تواند از هر مرتبه‌ای باشد اما در اکثر مواقع شما برای محاسبهرونسکین نیاز به تعیین مقدار دترمینان یک ماتریس دو در دو یا سه در سه هستید.

برای تسلط بیشتر بر این مباحث، می‌توانید  کپسول آموزشی معادلات دیفرانسیل لینوم را  مشاهده کنید.