چون در این مبحث ماتریس‌ها خیلی مهم هستن، یادآوری کنید که ماتریس‌های مربعی، قطر ماتریس‌ها، ضرب ماتریس‌ها، دترمینان ماتریس‌ها، ماتریس‌های بالا مثلثی، ترانهاده ماتریس‌ها، ماتریس‌های وارون و ... چی هستن!!!
حالا که این‌ها رو بلدید، یک دستگاه 3 معادله و 3 مجهول خطی (راستی خطی یعنی چجوری؟؟؟) مثال بزنید و سعی کنید این دستگاه رو تبدیل کنیید به یک معادله ماتریسی کهضرب دو تا ماتریس برابر بشه با یک ماتریس دیگه!!!
پس فهمیدیم که هر دستگاه خطی معادلات جبری رو میتونیم به صورت یک معادله ماتریسی به شکل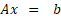
بنویسیم؛ و هدف بدست آوردن ماتریس (چون ستونی هست میتونیم بگیم بردار)
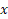هست ...
اولین ایده‌ای که به ذهنمون میرسه اینه که وارون ماتریس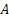 
رو حساب بکنیم و در دو طرف معادله ماتریسی‌مون ضربش بکنیم؛ ولی خب میدونیم که ماتریس وارون حساب کردن سخت و طولانی هست! پس میریم سراغ ایده دوم.
یک معادله ماتریسی دلخواه بنویسید، با این شرط که
بالا مثلثی باشه. بعد سعی از سطر آخر ماتریس ضرب کردن رو شروع بکنید و ببینید که معادله‌ها چقدر شیک و راحت حل میشن!!!
ولی همیشه که ماتریس ضرایب‌مون بالامثلثی نیست... چقدر خوب میشه اگر بتونیم اول با عملیات سطری ماتریس‌ها را بالا مثلثی کنیم، بعدش هم همینجوری آسون معادله‌ها رو حل بکنیم...
مژده این که میتونیم!!! چجوری؟؟ الان میگیم بهتون! کافیه اول یک ماتریس افزوده تشکیل بدیید؛ یعنی بردار جواب‌ها رو به آخر ماتریس ضرایبت (به عنوان آخرین ستون) اضافه بکنیید. به این ماتریس میگن یک ماتریس افزوده... حالا سطر اول رو توی یک عددی ضرب بکنید که اگر با سطر دوم جمع کنیید، درایه اول سطر دومت صفر بشه. پس ضرب کن و با سطر بعدی جمع کنید... برید سطر بعدی، توی یک عددی ضربش کنید که اگر با سطر جمع بشه درایه دومش صفر بشه!!! ضرب کنید و با بعدی جمع کنید... سطر به سطر اینکار رو بکنید و برید پایین تا تهش ماتریس بشه بالا مثلثی. بقیش رو هم که دیگه خودتون بهتر میدونید!!!
اگر هنوز احساس میکنین که درست کتوجه نشدین بهتون پیشنهاد میکنم کهکپسول آموزشی مارو ببینین حتما
به نظرتون به این روش میتونیم بگیم یک روش عددی؟؟؟ یادتون باشه که درس محاسبات عددی کارش با روش‌های عددیه...
دو روش عددی هم برای دستگاه معادلات خطی داریم. خیلی به هم شبیه هستن... اسم اولیش روش تکرار ژاکوبی هست... در این روش اول باید به ازای همه معادلات برید و از
امین معادله
رو تنها بکنید. یعنی ببریدش یک سمت معادله...
اگر ضریب
در معادله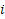
ام صفر بود، راه حلش چیه؟؟ می‌تونم جای معادله‌ها رو عوض کنیم؟؟؟
بعد باید برای هر کدوم از مجهولات دستگاه‌ت یک مقدار اولیه فرض کنید. با یکبار قرار دادن این اعداد در معادلاتی که بدست آورده بودید (همون ها که مجهولاتت رو تنها کردید)، هر کدوم از مجهولاتت یک قدم به مقدار واقعیشو نزدیک‌تر میشن!!! هر بار که مقادیر مرحله قبل رو بذارید داخل معادلات یک مقدار بهتر و دقیق‌تر تحویلتون میدن...
آیا در این روش تضمین همگرایی داریم؟؟ یعنی مطمئن باشیم که داریم به جواب نزدیک‌تر میشیم؟؟؟
اسم روش عددی بعدی روش گاوس– سایدل هست. فرق این روش با روش قبلی در این هست که در هر مرحله، موقع جایگذاری، اگر مقدار جدید مجهولی رو به دست آورده باشیم، در معادلات محاسبه مقدار جدید متغیر‌ها، همین مقدار جدید (مقداری که در همین مرحله به دست آوردیم) رو جایگذاری می‌کنیم و لزومی نداره که حتما مقدار مرحله قبل رو جایگذاری کنیم!!!
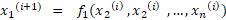
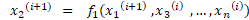
اون پرانتزهای بالای مجهولات نشون میدن که مقدار مجهول دو مرحله چندم تکرار مدنظرمونه.
به نظرتون روش تکرار ژاکوبی سریع‌تر به جواب میرسه یا روش گاوس - سایدل؟؟؟
روش گاوس - سایدل حتما به جواب میرسه؟؟ یعنی تضمین همگرایی داره یا نه؟؟؟
سعی کنید معادلات روش تکرار ژاکوبی رو هم مثل معادلاتی که برای روش گاوس - سایدل نوشتیم، بنویسید. (تنها فرقش همون پرانتزهای بالای مجهولات هست که توضیح دادیم چی رو نشون میده.)
و ده ها نکته ناگفته دیگه که فقط توی مثال های خاص میشه دید...با دیدنکپسول آموزشی محاسبات عددی میتونین در کمترین زمان تسلط خیلی خوبی توی این درس به دست بیارین.