2)روش حل توابعمختلط ، حدود و پیوستگی ، مشتق ، توابعتحلیلی

2-1 معرفی توابعمختلط و روش حل توابعمختلط
در این آموزش کپسولی لینوم، به سراغ یادگیری توابع مختلط، حدود و پیوستگی،مشتق و توابع تحلیلی میرویم.
برای شروع بهتر است که توابعمختلط را در قیاس با توابعحقیقی متناظر آن مقایسه کنیم :


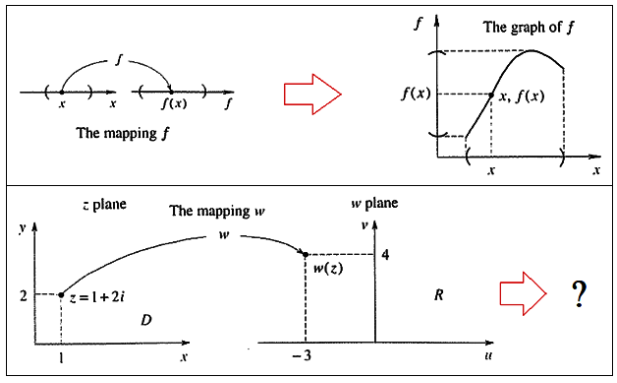
بنابراین در توابعمختلط چیزی به نام رسم تابع نداشته و صرفا به نگاشت یک ناحیه به ناحیه دیگر بسنده میکنیم.
به طور کلی صفحه 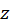 را صفحهدامنه و صفحه
را صفحهدامنه و صفحه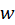 را صفحهبرد تابع
را صفحهبرد تابع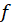 مینامند.
مینامند.
اگر 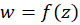 یک تابعمختلط باشد، آنگاه بخشهای حقیقی و موهومی آن را به ترتیب با
یک تابعمختلط باشد، آنگاه بخشهای حقیقی و موهومی آن را به ترتیب با 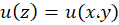 و
و 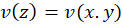 نمایشمیدهیم.
نمایشمیدهیم.

تعیین بخشهای حقیقی و موهومی توابعمختلط برای بررسی رفتارهای آن ها ضروری است و برای تعیین آنها از شکلهای دکارتی یا قطبی 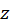 استفاده میشود.
استفاده میشود.
 مثال1) بخشهای حقیقی و موهومی تابع
مثال1) بخشهای حقیقی و موهومی تابع 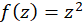 را بهدستآورید.
را بهدستآورید.
حل : با استفاده از شکل دکارتی 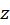 داریم :
داریم :
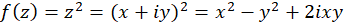
بنابراین
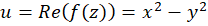 و
و 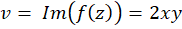
همچنین شکل قطبی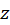 نتیجه میدهد:
نتیجه میدهد:
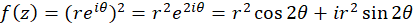
پس 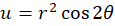 و
و 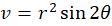 میباشند که همان
میباشند که همان 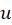 و
و 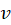 مختصات دکارتی است.
مختصات دکارتی است.
 مثال2) بخشهای حقیقی و موهومی تابع
مثال2) بخشهای حقیقی و موهومی تابع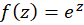 را بهدستآورید.
را بهدستآورید.
حل : با استفاده از شکل دکارتی داریم:
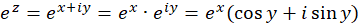
بنابراین
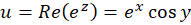 و
و 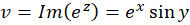
در اینجا شکل قطبی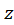 برای تعیین
برای تعیین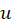 و
و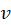 مناسب نیست.
مناسب نیست.
تعیین صفرهای تابع
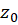 را صفر تابع
را صفر تابع 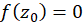 نامیم اگر باشد. برای تعیین صفرهای یک تابع کافی است بخشهای حقیقی و موهومی آن را تواما برابر صفر قراردهیم.
نامیم اگر باشد. برای تعیین صفرهای یک تابع کافی است بخشهای حقیقی و موهومی آن را تواما برابر صفر قراردهیم.
 مثال3)معادله
مثال3)معادله 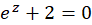 را حلکنید. (یعنی صفرهای تابع
را حلکنید. (یعنی صفرهای تابع 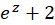 را بیابید.)
را بیابید.)
حل: با توجه به مثال2 نتیجه میگیریم که :
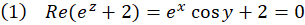
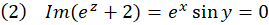
از رابطه (2) نتیجه میگیریم 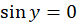 ، پس از رابطه (1) نتیجه میگیریم
، پس از رابطه (1) نتیجه میگیریم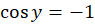 .حالت
.حالت 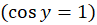 معادله ممتنع
معادله ممتنع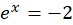 را نتیجه میدهد، پس
را نتیجه میدهد، پس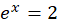
بنابراین 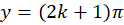 و
و 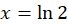 و جوابهای معادله برای کلیه
و جوابهای معادله برای کلیه 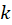 های صحیح به صورت زیر است :
های صحیح به صورت زیر است :
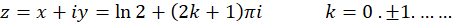
2-2 معرفی حدود و پیوستگی تابعمختلط و روش حل حدود و پیوستگی تابعمختلط
تعاریفحدود و پیوستگی توابعمختلط مشابه توابعحقیقی است. با توجه به اینکه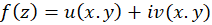 لذا اگر دو تابع دو متفییره
لذا اگر دو تابع دو متفییره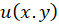 و
و 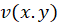 در نقطهای حد داشتهباشند، تابع
در نقطهای حد داشتهباشند، تابع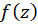 نیز در آن نقطه دارای حد است . ( و به همین ترتیب در مورد پیوستگی)
نیز در آن نقطه دارای حد است . ( و به همین ترتیب در مورد پیوستگی)
قضایای اساسی زیر در محاسبه حدود و تشخیص پیوستگی توابعمختلط مفیدند.
قضیه1-شرط لازم و کافی برای وجود حد تابع 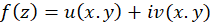 در
در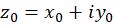 آن است که توابعحقیقی دو متغیره
آن است که توابعحقیقی دو متغیره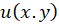 و
و 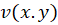 در
در 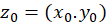 دارای حد باشند.
دارای حد باشند.
قضیه2-شرط لازم و کافی برای پیوستگی تابع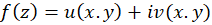 در
در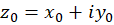 آن است که توابعحقیقی دو متغییره
آن است که توابعحقیقی دو متغییره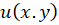 و
و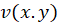 در
در 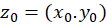 پیوسته باشند.
پیوسته باشند.
با توجه به قضایای فوق، چون بخشهای حقیقی و موهومی توابع چندجملهای در همه نقاط پیوسته اند، نتیجه میگیریم که توابع چندجملهای در همه نقاط پیوسته هستند. همچنین خارجقسمت دو چندجملهای ، تابع گویا، در همه نقاط به جز در ریشههای مخرج آن پیوسته است.
 مثال4)تحقیقکنید تابع
مثال4)تحقیقکنید تابع 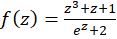 در چه نقاطی پیوسته است؟
در چه نقاطی پیوسته است؟
حل: تابع چندجملهای 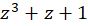 در کلیه نقاط پیوسته است. همچنین چون:
در کلیه نقاط پیوسته است. همچنین چون:
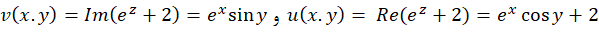 در کلیه نقاط پیوسته اند، پس تابع مخرج، در کلیه نقاط پیوسته است. بنابراین تابع در کلیه نقاط جز صفرهای مخرج یعنی نقاط برای کلیه های صحیح (مثال3) پیوسته است.
در کلیه نقاط پیوسته اند، پس تابع مخرج، در کلیه نقاط پیوسته است. بنابراین تابع در کلیه نقاط جز صفرهای مخرج یعنی نقاط برای کلیه های صحیح (مثال3) پیوسته است.
3-2 معرفی مشتق تابعمختلط و روش حل مشتق تابعمختلط و تابعتحلیلی
در ادامه اینآموزش کپسولی لینوم، مشتق توابعمختلط را مشابه توابعحقیقی تعریف میکنیم ، یعنی:
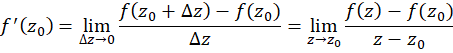
برای مشتقپذیری، تابع باید تک مقداری باشد یا تک مقداری بشود. اینکار با محدودکردن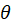 به یک دور مثلثاتی انجامپذیر است که معادل انتخاب
به یک دور مثلثاتی انجامپذیر است که معادل انتخاب 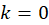 میباشد. اینکار مشابه انتخاب
میباشد. اینکار مشابه انتخاب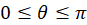 برای تابع نمودن
برای تابع نمودن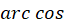 میباشد که در این صورت با
میباشد که در این صورت با 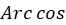 نمایشداده میشود.
نمایشداده میشود.
 مثال5)مشتقپذیری تابع
مثال5)مشتقپذیری تابع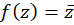 را بررسیکنید.
را بررسیکنید.
حل: در نقطه دلخواه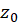 داریم:
داریم:
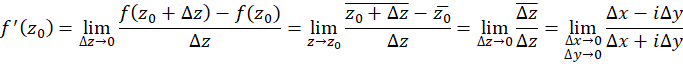
حد فوق روی مسیر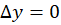 برابر مقدار 1 و روی مسیر برابر مقدار 1- است. پس حد فوق در هیچ نقطهای موجود نبوده و بنابراین
برابر مقدار 1 و روی مسیر برابر مقدار 1- است. پس حد فوق در هیچ نقطهای موجود نبوده و بنابراین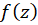 در هیچ نقطهای دارای مشتق نیست.
در هیچ نقطهای دارای مشتق نیست.
قضیه اول کوشی-ریمان (شرط لازم مشتقپذیری)

اگر تابع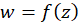 در نقطه
در نقطه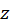 مشتقپذیر باشد، در این صورت حتما حد آن از دو مسیر (1) و (2) یکسان است. حال بررسی میکنیم برای یک تابع دلخواه
مشتقپذیر باشد، در این صورت حتما حد آن از دو مسیر (1) و (2) یکسان است. حال بررسی میکنیم برای یک تابع دلخواه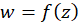 ، در چه صورت حد از این دو مسیر برابر خواهدشد.
، در چه صورت حد از این دو مسیر برابر خواهدشد.
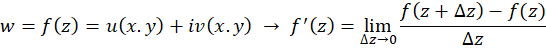
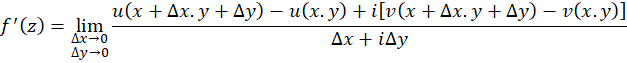
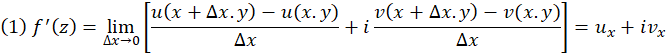
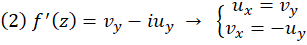
 مثال6)مشتقپذیری تابع
مثال6)مشتقپذیری تابع 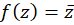 را بررسیکنید.
را بررسیکنید.
حل :
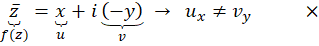
قضیه دوم کوشی-ریمان (شرط کافی مشتقپذیری)
اثبات دقیق این قضیه با استفاده از قضیه مقدار میانگین در توابع دو متغییره میباشد که طولانی بوده و از آن صرف نظر میشود. به جای آن یک اثبات شهودی برای این قضیه به صورت زیر ارائه میشود.
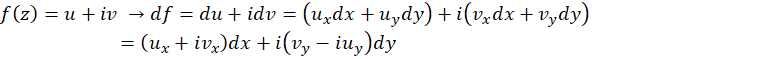
مشتق زنجیری زمانی اعتبار دارد که 6تابع 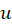 ,
, 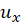
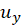
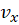
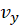 پیوسته باشند. حال اگر شرایط لازم کوشی-ریمان هم برقرار باشد، هر دو پرانتز بالا با هم مساوی اند. اگر هر دو را
پیوسته باشند. حال اگر شرایط لازم کوشی-ریمان هم برقرار باشد، هر دو پرانتز بالا با هم مساوی اند. اگر هر دو را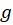 بنامیم:
بنامیم:
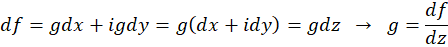
یعنی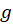 همان مشتق تابع
همان مشتق تابع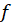 میباشد. پس اگر 6 تابع گفتهشده پیوسته و شرایط لازم کوشی-ریمان هم برقرار باشد ، تابع دارای مشتق بوده و به یکی از چهار فرم زیر قابل محاسبه است:
میباشد. پس اگر 6 تابع گفتهشده پیوسته و شرایط لازم کوشی-ریمان هم برقرار باشد ، تابع دارای مشتق بوده و به یکی از چهار فرم زیر قابل محاسبه است:
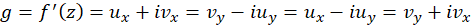
 مثال7)تحقیقکنید تابع
مثال7)تحقیقکنید تابع 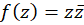 فقط در نقطه
فقط در نقطه 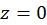 مشتقپذیر بوده و مشتق آن در این نقطه برابر صفر است.
مشتقپذیر بوده و مشتق آن در این نقطه برابر صفر است.
حل: چون 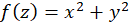 ، پس
، پس 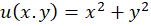 و
و 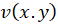 .
.
مشتقات نسبی برابرند با 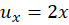 ،
، 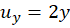 و
و 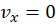 و
و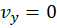
با قراردادن مشتقات در شرایط کوشی-ریمان داریم که باید و گردند. پس نقطه و و یا به عبارتی دیگر تنها نقطهای است که تابع در آن نقطه در شرایط کوشی-ریمان صدق میکند. علاوه بر آن چون مشتقاتجزئی در کلیه نقاط پیوسته اند ، پس تابع در این نقطه دارای مشتق است و داریم:
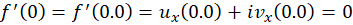
 مثال8)تحقیقکنید تابع
مثال8)تحقیقکنید تابع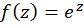 در کلیه نقاط دارای مشتق بوده و مشتق آن برابر خود تابع است.
در کلیه نقاط دارای مشتق بوده و مشتق آن برابر خود تابع است.
حل: درمثال2دیدیم که برای این تابع 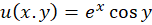 و
و 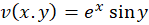 است. چون
است. چون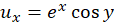 ،
، 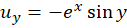 ،
، 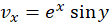 و
و 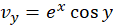 نتیجهمیگیریم که شرایط کوشی-ریمان در کلیه نقاط برقرار است. همچنین باتوجه به پیوستگی مشتقات جزئی
نتیجهمیگیریم که شرایط کوشی-ریمان در کلیه نقاط برقرار است. همچنین باتوجه به پیوستگی مشتقات جزئی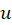 و
و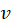 نتیجه میگیریم که
نتیجه میگیریم که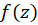 در کلیه نقاط مشتقپذیر است و
در کلیه نقاط مشتقپذیر است و
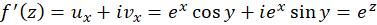
شرایط کوشی-ریمان در مختصاتقطبی
اگر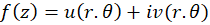 ، آنگاه با محاسبه شرایط کوشی در مختصات قطبی با فرض پیوستگی مشتقاتجزئی
، آنگاه با محاسبه شرایط کوشی در مختصات قطبی با فرض پیوستگی مشتقاتجزئی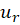 ،
، 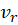 ،
، 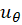
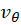 در یک همسایگی نقطه غیرصفر
در یک همسایگی نقطه غیرصفر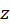 ، این شرایط به صورت زیر تبدیلمیشوند.
، این شرایط به صورت زیر تبدیلمیشوند.
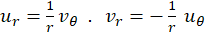
در این صورت مشتق تابع برابر است با :
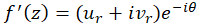
 مثال9)تحقیقکنید تابع
مثال9)تحقیقکنید تابع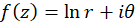 برای
برای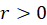 و
و 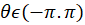 در شرایط کوشی صدقمیکند. مشتق تابع را تعیینکنید.
در شرایط کوشی صدقمیکند. مشتق تابع را تعیینکنید.
حل: تابع فوق در فاصله دادهشده پیوسته است. با محاسبه مشتقاتجزئی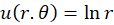 و
و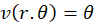 داریم:
داریم:
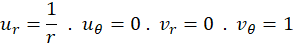
که در شرایط کوشی برای مختصات قطبی صدقمیکنند. چون مشتقاتنسبی مرتبهاول در فواصل دادهشده پیوسته اند، پس مشتق تابع برابر است با:
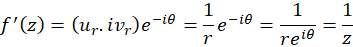
4-2 معرفی توابع تحلیلی و روش حل توابع تحلیلی

مفهوم تحلیلیبودن یک تابع به معنیمشتقپذیری در یک حوزه از صفحه مختلط است.
تابع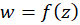 را در
را در تحلیلی مینامیم اگر همسایگی از
تحلیلی مینامیم اگر همسایگی از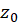 موجود باشد که در هر نقطه آن
موجود باشد که در هر نقطه آن 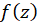 دارای مشتق گردد. در اینصورت
دارای مشتق گردد. در اینصورت 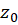 را یک نقطه عادی تابع مینامیم.
را یک نقطه عادی تابع مینامیم.
تابعی که در هر نقطه حوزه 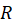 تحلیلی باشد، در
تحلیلی باشد، در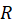 تحلیلی مینامند. تابعی که در کلِ اعدادمختلط تحلیلی باشد، تابعتام نامیدهمیشود. نقاط مرزی حوزهای که تابع در آن حوزه تحلیلی بوده ولی در خارج آن غیرتحلیلی است، نقاط تکین یانقاط منفرد نامیده میشوند. به عبارت دیگر:
تحلیلی مینامند. تابعی که در کلِ اعدادمختلط تحلیلی باشد، تابعتام نامیدهمیشود. نقاط مرزی حوزهای که تابع در آن حوزه تحلیلی بوده ولی در خارج آن غیرتحلیلی است، نقاط تکین یانقاط منفرد نامیده میشوند. به عبارت دیگر:
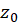 یک نقطه تکین تابع
یک نقطه تکین تابع 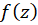 است اگر
است اگر 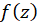 در
در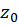 تحلیلی نبوده ولی در هر همسایگی از
تحلیلی نبوده ولی در هر همسایگی از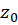 شامل نقاط تحلیلی از تابع گردد.
شامل نقاط تحلیلی از تابع گردد.
قضایای مشتقپذیری برای توابع تحلیلی نیز برقرارند، مثلا حاصلجمع ، تفاضل،حاصلضرب و ترکیب دو تابع تحلیلی ، تحلیلی است. خارجقسمت دو تابع تحلیلی ، تحلیلی است. خارجقسمت دو تابع تحلیلی به جز در صفرهای مخرج در سایر نقاط تحلیلی است.
 مثال10)تحقیقکنید توابع زیر در چه نقاطی تحلیلی هستند. نقاط تکین آنها را بیابید.
مثال10)تحقیقکنید توابع زیر در چه نقاطی تحلیلی هستند. نقاط تکین آنها را بیابید.
الف)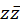 ب)
ب) 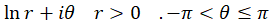 پ)
پ)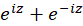 ت)
ت)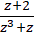
حل: الف) درمثال7 مشاهدهکردیم که این تابع در هیچ نقطهای دارای مشتق نیست. پس این تابع در هیچ نقطهای تحلیلی نبوده و بنابراین فاقد نقطه تکین است.
ب) درمثال9 مشاهدهکردیم که این تابع در کلیه نقاط جز مبدا مختصات و نیممحور منفی محور حقیقی، یعنی در کلیه نقاط جز نقاطی که برای آنها 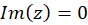 و
و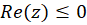 مشتقپذیر است. پس در این ناحیه تحلیلی نیز هست و نقاط تکین آن همان نقاطی هستند که تابع در آنها تحلیلی نیست.
مشتقپذیر است. پس در این ناحیه تحلیلی نیز هست و نقاط تکین آن همان نقاطی هستند که تابع در آنها تحلیلی نیست.
پ) چون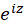 ترکیب دو تابع تام و است، بنابراین تابعی تام است. به همین نحو نیز تابعی تام است. پس حاصل جمع آنها تابعی تام بوده و فاقد نقطه تکین است.
ترکیب دو تابع تام و است، بنابراین تابعی تام است. به همین نحو نیز تابعی تام است. پس حاصل جمع آنها تابعی تام بوده و فاقد نقطه تکین است.
ت) تابع فوق خارجقسمت دو چندجملهای بوده و بنابراین در کلیه نقاط جز ریشههای مخرج یعنی نقاط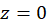 ،
،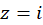 و
و 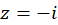 مشتقپذیر است. پس در سایر نقاط تحلیلی بوده و این سه نقطه، نقاط تکین تابع میباشند.
مشتقپذیر است. پس در سایر نقاط تحلیلی بوده و این سه نقطه، نقاط تکین تابع میباشند.
نقطه تکین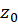 را یک نقطهتکین تنهامینامیم اگر همسایگی از نقطه
را یک نقطهتکین تنهامینامیم اگر همسایگی از نقطه 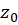 موجود باشد که در آن همسایگی تنها نقطه تکین تابع نقطه
موجود باشد که در آن همسایگی تنها نقطه تکین تابع نقطه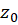 باشد.
باشد.
در غیر اینصورت نقطه تکین راغیرتنهانامند.
نقاط تکین تابع ت) همگی تنها هستند ولی نقاط تکین تابع ب) همگی غیرتنها میباشند.
توابع تحلیلی دارای خواص بسیار خواص بسیار مهم و مفیدی هستندکه ما به یکی از آنها اشاره میکنیم:
اگر بخشهای حقیقی و موهومی تابع تحلیلی 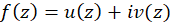 در حوزه
در حوزه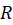 ، دارای مشتقات نسبی مرتبهدوم پیوسته باشند، این بخشها در معادلهپتانسیل
، دارای مشتقات نسبی مرتبهدوم پیوسته باشند، این بخشها در معادلهپتانسیل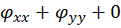 در آن حوزه صدقمیکنند، یعنی :
در آن حوزه صدقمیکنند، یعنی :
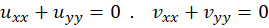
تابعی که دارای مشتقات مرتبهدوم پیوسته بوده و در معادله پتانسیل صدق کند ، تابعهارمونیک یا همساز نامیده میشود.
بخشهای حقیقی و موهومی تابع تحلیلی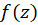 همساز هستند. در اینصورت
همساز هستند. در اینصورت 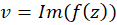 را مزدوج هارمونیک یامزدوجهمساز
را مزدوج هارمونیک یامزدوجهمساز 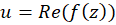 میخوانند.
میخوانند.
 مثال11)مزدوج همساز
مثال11)مزدوج همساز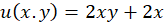 را تعیین کرده و آنرا
را تعیین کرده و آنرا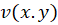 بنامید. اگر
بنامید. اگر 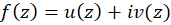
و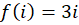 ،
،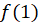 را تعیین کرده و سپس
را تعیین کرده و سپس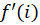 را بهدستآورید.
را بهدستآورید.
حل: با استفاده از شرایط کوشی داریم:
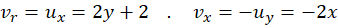
با انتگرالگیری از دو رابطه نتیجه میگیریم:

با مقایسه روابط فوق داریم:

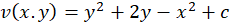
مزدوج همساز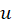 است. از طرفی :
است. از طرفی :
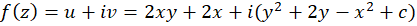
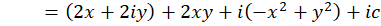
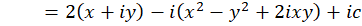
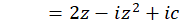
چون 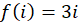 ، پس:
، پس:
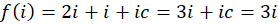
و یا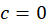 ، بنابراین
، بنابراین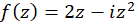 و
و 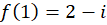 . همچنین:
. همچنین:
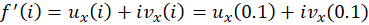
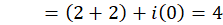
به طور کلی میتوان نشانداد که هرگاه تابع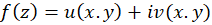 تحلیلی باشد، آنگاه آن را میتوان به صورت زیر نوشت:
تحلیلی باشد، آنگاه آن را میتوان به صورت زیر نوشت:
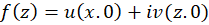
کافی است توجهکنیم که اگر 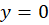 باشد، آنگاه :
باشد، آنگاه :
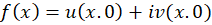
حال با جانشینی به جای نتیجه بالا بهدستمیآید. از این خاصیت برای تعیین سریعتر تابع استفاده میکنیم، به عنوان مثال در این مثال:
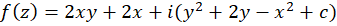
با جانشینی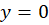 و
و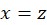 نتیجهمیگیریم:
نتیجهمیگیریم:
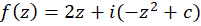
که همان نتیجه قبل است.
برای یادگیری بیشتر مبحثاعداد مختلط، میتوانید ویدیوآموزش اعداد مختلط را ببینید.