معادلات قابل تبدیل به معادله خطی با ضرایب ثابت

در آموزش گذشته، با معادلات خطی همگن و ناهمگن مرتبه دوم آشنا شدیم. در این آموزش کپسولی لینوم، قصد داریم به سراغ یادگیریمعادلات قابل تبدیل به معادله خطی با ضرایب ثابت برویم.
دستهای از معادلات هستند که خطی و دارای ضرایب ثایت نیستند ولی میتوان آن ها را به معادلات خطی با ضرایب ثابت تبدیل کرد که در ادامه به بررسی آنها خواهیمپرداخت:
1- معادله دیفرانسیل کوشی-اویلر
این معادلات به فرم کلی زیر میباشند:
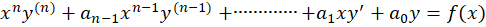
که در آن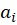 ها اعدادی ثابت هستند.
ها اعدادی ثابت هستند.
فرم تعمیم یافته معادله کوشی اویلر به صورت زیر است:
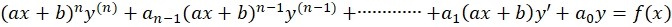
روش حل معادله دیفرانسیل کوشی-اویلر
با تغییر متغیر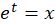 میتوان معادلات کوشی اویلر را به معادلاتی با ضرایب ثابت تبدیل کرد. در اینجا میخواهیم حالت خاصمعادلات کوشی اویلر که به صورت زیر است را بررسی کنیم:
میتوان معادلات کوشی اویلر را به معادلاتی با ضرایب ثابت تبدیل کرد. در اینجا میخواهیم حالت خاصمعادلات کوشی اویلر که به صورت زیر است را بررسی کنیم:
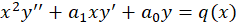
اگر از تغییر متغیر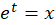 استفاده کنیم، معادله فوق به شکل زیر تبدیل خواهد شد:
استفاده کنیم، معادله فوق به شکل زیر تبدیل خواهد شد:
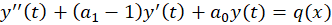
سپس باید با مشخص کردن معادله مشخصه این عبارت و تعیین ریشههای آن،جواب عمومی معادله همگن شده را بر حسب 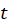 بهدست آورید و در نهایت به جای
بهدست آورید و در نهایت به جای 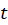 ،
، 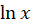 قرار دهید.
قرار دهید.
برای بهدست آوردن جواب خصوصی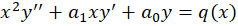 هم از روشهایی که پیش از این گفته شده استفاده نمایید و در پایان به جای
هم از روشهایی که پیش از این گفته شده استفاده نمایید و در پایان به جای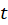 ،
،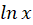 قرار دهید.
قرار دهید.
توجه کنید که اگر با فرم تعمیم یافته معادله کوشی-اویلر روبرو شدید، باید از تغییر متغیر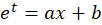 استفاده کنید و طبیعتا در نهایت برای بهدست آوردن جواب معادله اصلی به جای
استفاده کنید و طبیعتا در نهایت برای بهدست آوردن جواب معادله اصلی به جای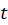 ،
،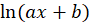 قرار دهید.
قرار دهید.
 مثال) معادله
مثال) معادله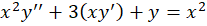 را حل کنید.
را حل کنید.
تغییر متغیر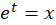 را انجام میدهیم و معادله به فرم زیر تبدیل میگردد:
را انجام میدهیم و معادله به فرم زیر تبدیل میگردد:
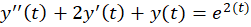
اکنون جواب عمومی معادله بدست آمده درحالت همگن را بهدست میآوریم:
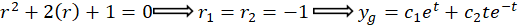
اکنون جواب خصوصی معادله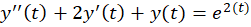 را بهدست میآوریم . ما با توجه به سهولتروش اپراتور معکوس از آن استفاده میکنیم اما شما میتوانید جواب خصوصی را از راه های دیگر نیز بهدست آورید:
را بهدست میآوریم . ما با توجه به سهولتروش اپراتور معکوس از آن استفاده میکنیم اما شما میتوانید جواب خصوصی را از راه های دیگر نیز بهدست آورید:
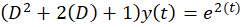
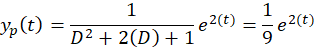
حال نوبت به محاسبه جواب عمومی معادله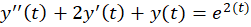 رسیدهاست:
رسیدهاست:
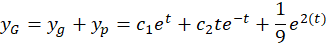
و در نهایت برای بهدست آوردنجواب عمومی معادله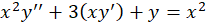 باید به جایt
باید به جایt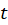 ،lnx
،lnx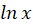 قرار دهیم:
قرار دهیم:
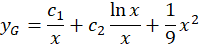
حل معادلات دیفرانسیلی کوشی-اویلر در حالت همگن

این دسته از معادلات را به همان روش قبلی که به آن اشاره کردیم نیز میتوان حل کرد ولی در این جا سعی میکنیم که روش سریعتری برای حل این معادلات درحالت همگن ارائه کنیم.
برای حل این دسته از معادلات کافیست قرار دهید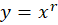 و با توجه به همین رابطه
و با توجه به همین رابطه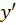 و
و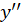 را نیز بهدستآورید.سپس به عبارتی به صورت زیر خواهید رسید:
را نیز بهدستآورید.سپس به عبارتی به صورت زیر خواهید رسید:
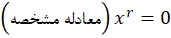
پس این روش به ما کمک میکند به سرعت معادله مشخصه را بهدست آوریم. سپس با توجه به اینکه ریشه های معادله مشخصه به چه صورت است جواب معادله به یکی از صورتهای زیر است:
1-اگر معادله مفسر دارای ریشههای متمایز به صورت 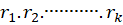 باشد، آنگاه جواب عمومی معادله به صورت زیر خواهد بود:
باشد، آنگاه جواب عمومی معادله به صورت زیر خواهد بود:
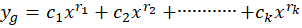
2-اگر 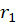 ریشه تکراری مرتبه
ریشه تکراری مرتبه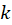 ام معادله مشخصه باشد:
ام معادله مشخصه باشد:
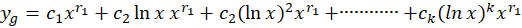
3-اگر معادله دارای ریشه مختلط به صورت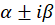 باشد باید عبارت
باشد باید عبارت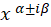 را به صورت زیر بنویسید:
را به صورت زیر بنویسید:
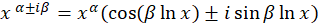
 مثال) جواب عمومی معادله دیفرانسیل
مثال) جواب عمومی معادله دیفرانسیل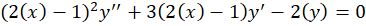 را بیابید.
را بیابید.
قرار میدهیم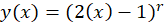 :
:
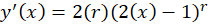
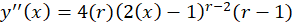
معادله مشخصه به صورت زیر بهدست میآید:
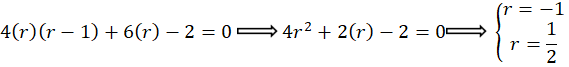
و جواب عمومی برابر است با:
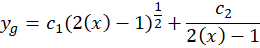
2- اگر معادلهای به فرم زیر داشتهباشیم:
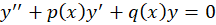
اگر در این معادلات، عبارت مقابل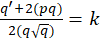 که در آن
که در آن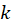 عدد ثابتی است برقرار باشد؛ آنگاه معادله فوق با تغییر متغییری به شکل
عدد ثابتی است برقرار باشد؛ آنگاه معادله فوق با تغییر متغییری به شکل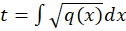 به معادلهای بهضرایب ثابت با فرم زیر تبدیل خواهد شد:
به معادلهای بهضرایب ثابت با فرم زیر تبدیل خواهد شد:
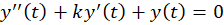
 مثال) جواب عمومی معادله
مثال) جواب عمومی معادله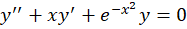 را بهدستآورید.
را بهدستآورید.
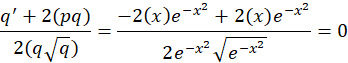
حاصل این عبارت دو چیز را برای ما مشخص میکند. اولین موضوع این که عددی ثابت است پس میتوان از تغییر متغیر مد نظر ما یعنی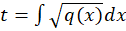 استفاده نمود. موضوع دوم هم این که مقدار
استفاده نمود. موضوع دوم هم این که مقدار 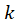 برابر با صفر است.پس معادله به شکل زیر تبدیل خواهد شد:
برابر با صفر است.پس معادله به شکل زیر تبدیل خواهد شد:
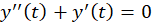
و جواب عمومی برابر است با:
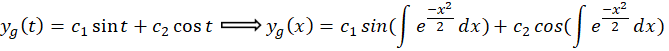
سری توانی

اگر فرض کنیم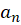 دنبالهای در اعداد حقیقی و
دنبالهای در اعداد حقیقی و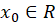 دلخواه باشد،
دلخواه باشد،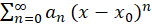 را یک سری توانی حول
را یک سری توانی حول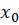 میگوییم.
میگوییم.
شعاع همگرایی
به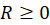 شعاع همگرایی سری توانی
شعاع همگرایی سری توانی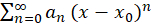 میگوییم هر گاه سری به ازای
میگوییم هر گاه سری به ازای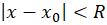 همگرا و به ازای
همگرا و به ازای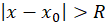 واگرا باشد.
واگرا باشد.
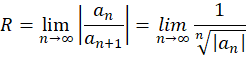
به سه نکته زیر توجه کنید:
1-به ازای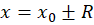 نمی توان درباره ی همگرایی و واگرایی سری اظهار نظر کرد.
نمی توان درباره ی همگرایی و واگرایی سری اظهار نظر کرد.
2-اگر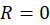 سری فقط به ازای
سری فقط به ازای 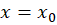 همگرا است.
همگرا است.
3-اگر 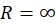 سری به ازای هر
سری به ازای هر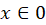 همگرا است.
همگرا است.
 مثال) شعاع و بازه همگرایی
مثال) شعاع و بازه همگرایی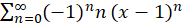 را حساب کنید.
را حساب کنید.
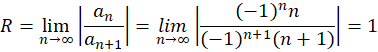
با توجه به صورت سوال متوجه میشویم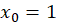 پس داریم:
پس داریم:
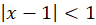
همان طور که پیش از این گفتیم به ازای 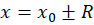 نمیتوان درباره یهمگرایی و واگرایی سری اظهار نظر کرد و باید شرایط در این دو نقطه را به صورت جداگانه بررسی کرد:
نمیتوان درباره یهمگرایی و واگرایی سری اظهار نظر کرد و باید شرایط در این دو نقطه را به صورت جداگانه بررسی کرد:
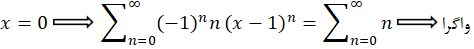
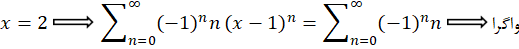
از سه عبارت بالا بازه همگرایی به صورت زیر نتیجهگیری میشود:
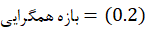
قضیه
اگر فرض کنیم سری توانی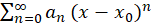 در بازه
در بازه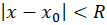 همگرا باشد آنگاه انتگرالگیری و مشتقگیری از این سری توانیدامنه همگرایی آن را تغییر نمیدهد.
همگرا باشد آنگاه انتگرالگیری و مشتقگیری از این سری توانیدامنه همگرایی آن را تغییر نمیدهد.
سری تیلور
تعریف
سری تیلور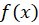 حول
حول 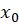 را به شکل زیر تعریف میکنیم:
را به شکل زیر تعریف میکنیم:
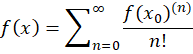
سری تیلور حول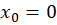 را سری مک لورن مینامیم.
را سری مک لورن مینامیم.
برای تسلط بیشتر بر این مباحث، میتوانید کپسول آموزشی معادلات دیفرانسیل لینوم را مشاهده کنید.