نقاط معمولی(تحلیلی) و منفرد(تکین)

در آموزش گذشته بامعادلات دیفرانسیل قابل تبدیل به معادله خطی با ضرایب ثابت آشنا شدیم. در این آموزش نیز قصد داریم تا در رابطه با نقاط معمولی و منفرد صحبت کنیم.

تعریف

نقطهx0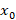 را یک نقطهتحلیلی برای تابع 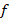می نامیم هر گاه تابع 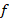حول آن دارای بسط تیلور باشد.

مثال: برای تابع همه نقاط ، نقاطی عادی هستند به جز نقطه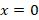 که یک نقطه منفرد برای آن است.

تعریف

اگر یک معادله دیفرانسیل به شکل زیر داشته باشیم:

آنگاه نقطه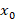 یک نقطه عادی برای اینمعادله دیفرانسیل است اگر 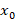 برای تمامی توابع زیر یک نقطه عادی باشد:

-کلیه توابع 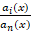در بازه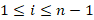

-تابع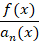

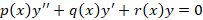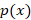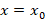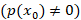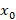در حالت خاص اگر معادله ای به صورتداشته باشیم ، اگربه ازایمخالف صفر باشدآنگاهیک نقطه تحلیلی برای معادله فوق است.

 

مثال: نقطه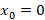 برای معادله دیفرانسیل 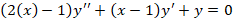 چگونه نقطه ای است؟

برای ساده تر شدن حل بهتر است ابتدا معادله را بهفرم کانونی بنویسیم یعنی به گونه ای که ضریبy''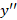 برابر با یک باشد پس داریم:

 

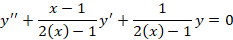
حال با توجه به این که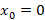 برای دو تابع  و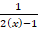 یک نقطه عادی می باشد پس برای معادله نیز یک نقطه عادی است.

حل معادلات دیفرانسیل با سری های توانی

اگر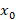 یک نقطه عادی برای معادله دیفرانسیل باشد در این صورت جواب معادله به صورت سری توانی است.کلید حل این معادلات بدست آوردن ضرایب سری توانی یعنی 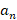ها است.این ضرایب را می توان از دو راه متفاوت محاسبه کرد:

1-روش مشتقات متوالی

2-روش نوشتن جواب به صورت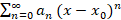 y=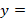

روش مشتقات متوالی

چنان چه نقطه 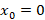 یک نقطه عادی برای معادله دیفرانسیل باشد  آنگاه این معادله در نقطه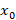 دارای بسط تیلور است یعنی جواب معادله دیفرانسیل فوق را می توان به صورت زیر نوشت:

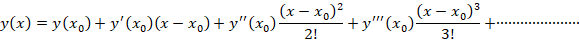
اکنون با مشتق گیری متوالی از معادلات دیفرانسیل داده شده مقادیر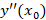 و ............ را بدست می آوریم و فرم جواب را استخراج می کنیم.معمولا بدست آوردن چهار یا پنج جمله اول کفایت می کند.

 

روش نوشتن جواب به صورت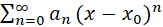 

در این روش باید تابع جواب را به صورت بنویسیم و مشتقات آن را به ترتیب زیر محاسبه کنیم :

سپس آن ها را در معادله جایگذاری می کنیم.در گام بعد باید توابعی مانند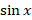  و ....... که رد معادله هستند را حول نقطه 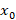بسط دهیم.

نهایتا با برابر قراردادن ضرایب طرفین معادله حاصل ضرایب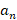 استخراج می گردد.

مثال: معادله دیفرانسیل را حل کنید.

با توجه به این که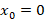 برای معادله فوق است پس می توانیم از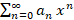 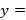استفاده کنیم بنا براین داریم:

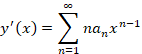
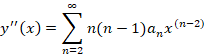
اکنون در معادله جایگذاری می کنیم:

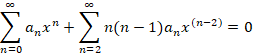
حال اندیس را از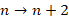 تغییر می دهیم و معادله فوق به صورت زیر تغییر می کند:

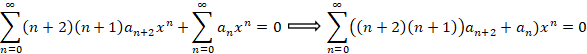
با توجه به معادله فوق فرمول بازگشتی زیر حاصل می شود که با استفاده از آن ها می توان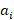 ها را محاسبه نمود:

بابا توجه به فرمول فوق روابط زیر بین ضرایب برقرار است:

 

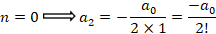
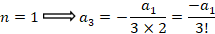
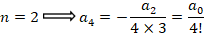
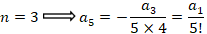
با توجه به فرم کلی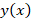 که به صورت 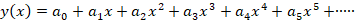است پس جواب را به صورت زیر می نویسیم:

 

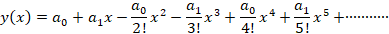
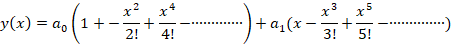
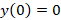مثال: با فرض این که و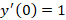 معادله دیفرانسیل 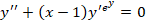را حل کنید.

اگر قرار دهید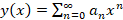 و شروع به حل معادله کنیم متوجه خواهیم شد که مسیر حل با این روش پیچیده خواهد بود لذا ما برای حل معادله از روش مشتقات متوالی استفاده می کنیم:

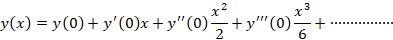
مقدار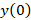 و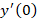 را خود سوال مشخص کرده است.برای بدتس آوردن 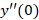باید نقطه صفر را در معادله جایگذاری کنیم:

 

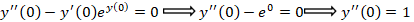
حالا برای محاسبه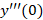 کافیست از معادله دیفرانسیل مشتق بگیریم:

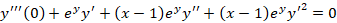
با جایگذاری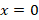 در معادله فوق داریم:

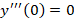
و جواب معادله با توجه به مقادیر بدست آمده به شکل زیر است:

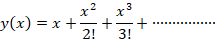
انواع نقطه تکین (منفرد)

1-تکین منظم

2-تکین نا منظم

تکین منظم

اگر یک معادله به شکل زیر داشته باشیم:

در ابتدا باید با توجه به روابطی که پیش از این به آن ها اشاره شده است بررسی کنید که نقطه مورد نظر یک نقطه عادی برای معادله است یانقطه منفرد.در صورتی که  منفرد بود اگر برای کلیه توابع زیر یک نقطه عادی باشد آن گاه یک نقطه منفرد منظم است:

1-کلیه توابع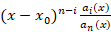 در بازه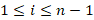

2-تابع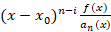 

در حالت خاص که با یک معادله مرتبه دوم به شکل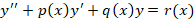 روبرو هستیم در صورت تکین بودن 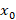در صورتی منظم است که برای سه تابع زیر نقطه عادی باشد:

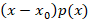
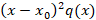
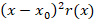
تکین نامنظم

نقاطی که تکین منظم نیستند ، تکین نا منظم هستند.

 

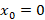مثال: نوع نقاط منفرد و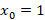 را در معادله 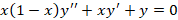را مشخص کنید.

ابتدا فرم کانونی معادله را می نویسیم:

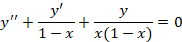
سپس توابعی که باید عادی بودن نقاط تکین معادله اصلی را در آن ها بررسی کنیم تا  منظم یا غیر منظم بودن نقطه های مورد بررسی را متوجه شویم مشخص می کنیم.

برای نقطه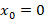 داریم:

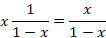
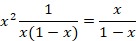
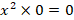
نقطه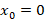 نقطه ای عادی برای هر سه تابع فوق است پس 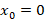یک نقطه تکین منظم برای معادله است.حالا به بررسی نقطه 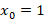می پردازیم:

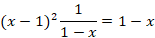
نقطه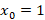 نقطه ای عادی برای هر سه تابع فوق است پس 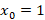یک نقطه تکین منظم برای معادله است.

---

برای تسلط بیشتر بر این مباحث، می‌توانید  کپسول آموزشی معادلات دیفرانسیل لینوم را  مشاهده کنید.