تبدیل لاپلاس

 

تعریف

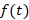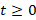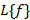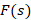تبدیلات نقش بسیار مهمی در حلمسائل مهندسی دارند و قصد ما در این جا تحلیل یک تبدیلانتگرالی به نامتبدیل لاپلاس است.اگر فرض کنیم به ازای تعریف شده باشد ، تبدیل لاپلاس را با نماد یا نشان می دهیم و آن را به صورت زیر تعریف می کنیم:

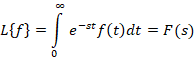
همچنین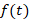 را تبدیل لاپلاس معکوس 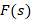می نامیم و به صورت زیر نمایش می دهیم:

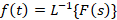
لاپلاس توابع مقدماتی

لاپلاس را با توجه به رابطه ای که بیان شد می توان برای توابع مختلف بدست آورد ولی برای حل برخی مسائل با توجه به اینکه روند حل بسیار طولانی دارند می بایست نتیجه نهایی محاسبه لاپلاس برخی توابع را در خاطر داشته باشیم و بدون انجاممحاسبات از جواب نهایی آن ها برای حل مسائل استفاده کنیم که برخی از این توابع در ادامه آورده شده اند:

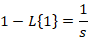
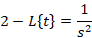
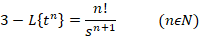
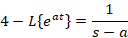
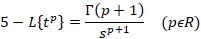
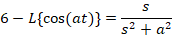
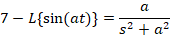
خواص تبدیل لاپلاس

1-تبدیل لاپلاس و معکوس آن عملگر های خطی هستند یعنی داریم:

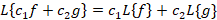
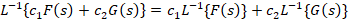
توجه داشته باشید که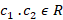 می باشند.

2-با توجه به مورد اول رابطه زیر برقرار است:

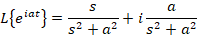
3-برای کسینوس و سینوس هایپربولیک داریم:

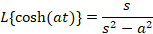
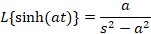
4-یکی دیگر از خواص تبدیل لاپلاس خاصیت انتقال است که بیان می کند چنانچه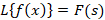 باشد در این صورت:

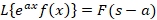
و خاصیت انتقال دوم نیز بیان می کند که اگر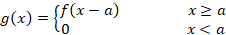 آنگاه رابطه زیر برقرار است:

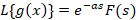
5-تبدیلات لاپلاس خاصیتی به نام تغییر مبنا دارند که منظور از آن عبارت زیر است:

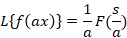
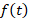مثال: لاپلاس تابع و لاپلاس معکوس تابع 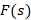را بیابید.

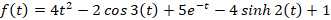
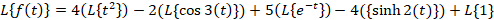
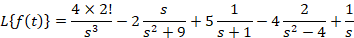
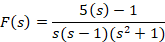
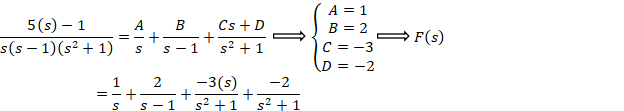
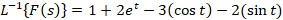
مثال: تابعی را بیابید که تبدیل لاپلاس آن به صورت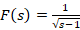 باشد.

 

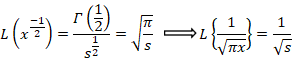
بنا بر قضیه انتقال داریم:

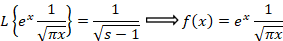
6-تبدیل لاپلاس مشتقات تابع

اگر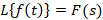 باشد آنگاه روابط زیر برقرار است:

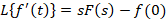
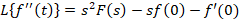
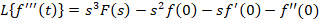
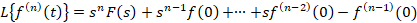
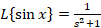مثال: اگر بدانیم   در این صورت 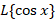 را بیابید.

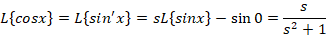
7-به ازای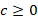 تابع پله ای واحد را به صورت زیر تعریف می کنیم:

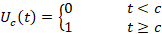
8-پیچش دو تابع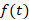 و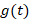 را به صورت 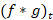نمایش می دهیم و داریم:

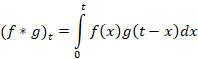
پیچش دارای خواص زیر می باشد:

1-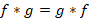 

2-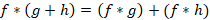

3-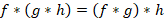

4-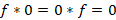

5-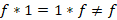

9-اگر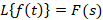 و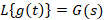 آنگاه داریم:

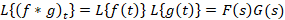
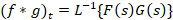
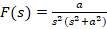مثال: لاپلاس وارون را بدست آورید.

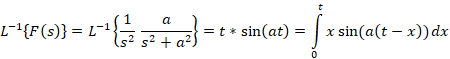
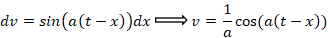
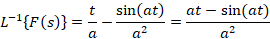
10-اگر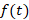 یک تابع متناوب با دوره تناوب 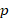باشد یعنی 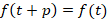آنگاه رابطه زیر برقرار است:

 

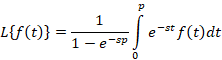
تابع دلتای دیراک

اگر عبارتی به صورت زیر داشته باشیم:

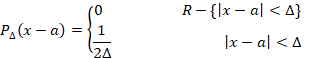
در این صورت 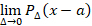  را تابع دلتای دیراک می نامند و آن را به فرم 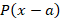نشان می دهند که برابر است با:

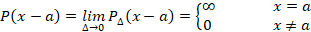
محاسبه لاپلاس توابع چند ضابطه ای

اگر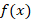 یک تابع چند ضابطه ای باشد که به صورت زیر تعریف شده است:

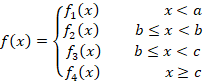
در این صورت برای محاسبه تبدیل لاپلاس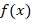 ابتدا باید آن را با استفاده ازتابع پله ای واحد به صورت زیر بازنویسی کنیم:

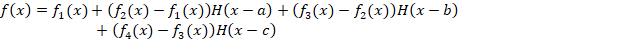
و نهایتا از طرفین لاپلاس می گیریم.

مثال: اگر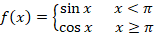 باشد لاپلاس تابع 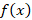را محاسبه کنید.

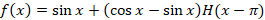
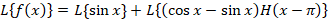
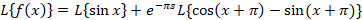
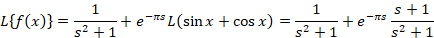
تبدیل معکوس لاپلاس

با توجه به توضیحات داده شده در موردتبدیل لاپلاس خواص بسیاری از تبدیل معکوس لاپلاس نیز قابل محاسبه است ولی ما برای سادگی کار شما تعدادی از این خاصیت ها را در ادامه نام می بریم:

1-خاصیت خطی تبدیل معکوس لاپلاس:

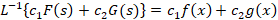
2-خاصیت انتقال تبدیل لاپلاس معکوس:

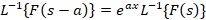
3-خاصیت انتگرال پیچشی تبدیل لاپلاس معکوس:

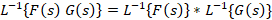
4-در این جا هم برای لاپلاس و هم لاپلاس معکوس رابطه هایی را بیان می کنیم:

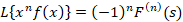
برای لاپلاس معکوس از یکی از دو رابطه زیر می توانید استفاده نمایید:

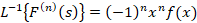
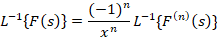
مثال: تبدیل لاپلاس معکوس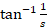 را بیابید.

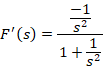
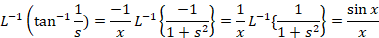
5-خاصیت پنج و آخرین خاصیتی که از لاپلاس معکوس بیان می کنیم مربوط به تابع پله ای واحد یاهوی ساید می باشد:

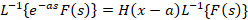
روش های محاسبه تبدیل لاپلاس

 

1-استفاده از تعریف تبدیل لاپلاس یا روش مستقیم

2-روش معادله دیفرانسیل

3-روش بسط سری

4-استفاده از قضایای مربوط به تبدیل لاپلاس

استفاده از تعریف تبدیل لاپلاس یا روش مستقیم

اگر تابعی جزوتوابع مرسوم نبود معمولا تبدیل لاپلاس آن ها را از روش مستقیم محاسبه می کنیم.

مثال: تبدیل لاپلاس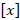 را محاسبه کنید.

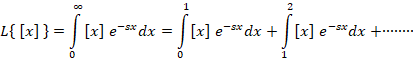
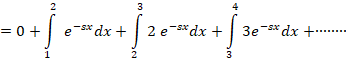
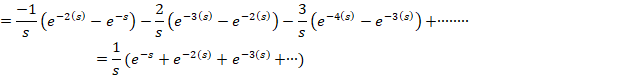
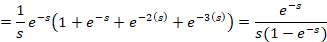
روش معادله دیفرانسیل

در این روش ابتدا معادله دیفرانسیل تابعی که تبدیل لاپلاس آن خواسته شده است را بدست می آوریم سپس بالاپلاس گیری از طرفین معادله دیفرانسیل حاصل و با استفاده از قضیه هایی که پیش از این به آن ها اشاره شد تبدیل لاپلاس مورد نظر را بدست می آوریم.

مثال: تبدیل لاپلاس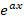 را بیابید.

با توجه به این که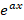 جواب معادله دیفرانسیل 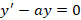است داریم:

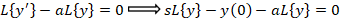
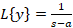
روش بسط سری

در این روش بسط تابع داده شده را حول نقطه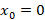 می نویسیم سپس جمله به جملهتبدیل لاپلاس می گیریم و از قاعده ی 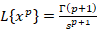استفاده کرده و جواب را می یابیم.

مثال: تبدیل لاپلاس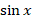 را با روش بسط سری بیابید.

---

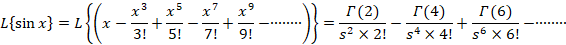
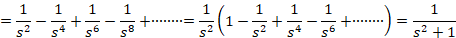
برای تسلط بیشتر بر این مباحث، می‌توانید  کپسول آموزشی معادلات دیفرانسیللینوم را  مشاهده کنید.