دنباله‌ها و سری‌ها
در اینآموزش ریاضی دولینوم، به سراغ یادگیری دنباله‌ها و سری‌ها می‌رویم.
دنباله نامتناهی
فرض می‌کنیم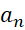
یک دنباله و
تابعی باشد, به طوری که به ازای هر
اگر
آنگاه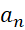
همگراست و
اگر
, آنگاه
واگراست و
بنابراین
.
اگر
و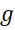
تابع باشد که در
پیوسته است, آنگاه
خواهد بود.
دنباله 
را یکدنباله هندسی با قدرنسبت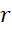
می‌گوییم.
دنباله هندسی
به ازای
و
و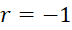اگراست.
اگر
آنگاه
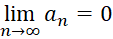خواهد شد.
دنباله
را کراندار می‌نامیم اگر عددی چون
وجود داشته‌باشد به طوری که به ازای آن داشته‌باشیم : 
.
قضیه
اگر
همگرا باشد, آنگاه 
کراندار خواهد بود.
اگر
کراندار نباشد,آنگاه
واگرا است.
تعریف
دنباله
رایکنوا گوییم هرگاه یکی از دوحالت زیر برای آن پیش بیاید:
1) به ازای هر
,
باشد که به آن دنبالهیکنوای غیر‌‌کاهشی گویند.
2) به ازای هر
,
باشد که به آن دنبالهیکنوای غیرافزایشی گویند.
دنباله کراندار و یکنوا, همگراست.
در این قسمت ازآموزش لینوم، به سراغ سری‌ها می‌رویم.
سری نامتناهی
عبارت به صورت
را یکسری نامتناهی گوییم.
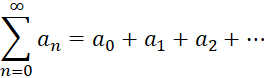
اگر سری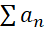
همگرا باشد, آنگاه
خواهد بود.
اگر
باشد و یا وجود نداشته‌باشد, آنگاه سری
واگراست.
سری
را سری همسار می‌گویند و واگراست.
سری به صورت
را که در آن
و
اعداد حقیقی هستند و
باشد را یک سری هندسی می‌نامیم. 
را جمله اول و
را قدرنسبت این سری هندسی می‌گوییم. 
اگر سری 
واگرا و سری
همگرا باشد در این صورت یکی از دوحالت زیر را خواهیمداشت:
الف)
یک سری واگراست.
ب) اگر
, عددی ناصفر باشد آنگاه سری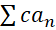 
نیز واگراست.
سری های با جملات نامنفی
اگر
یک سری با جملات نامنفی و 
مجموع جزئی
ام آن باشد, در این صورت سری 
اگر و فقط اگر دنباله
کراندار باشد.
آزمون انتگرال
اگر
یک سری و
یک تابع باشد که به ازای
نامنفی,پیوسته و کاهشی باشد و به ازای مقادیر
,fn=an
در این صورت دو حالت زیر راخواهیم‌داشت:
الف) 
همگراست اگر انتگرال ناسره
همگرا باشد.
ب)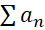
واگراست اگر
واگرا باشد.
قضیه مهم
سری 
همگراست اگر و فقط اگر 
باشد.
این سری در صورتی که 
باشد, واگراست.
آزمون مقایسه
فرض کنید
و
دو سری با جملات نامنفی باشند. در این صورت خواهیمداشت:
الف) اگر
همگرا باشد و به ازای هر
,
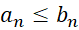باشد, آنگاه
نیز همگراست و خواهیم داشت:
ب) اگر
واگرا باشد و به ازای هر
,
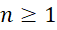باشد, آنگاه
نیز واگراست.
آزمون مقایسه حدی
اگر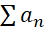
و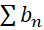
دوسری باشند به طوری که به ازای هر
,
و
باشد در این صورت خواهیمداشت:
الف) اگر
( درواقع
), آنگاه یا هردو سری همگرا و یا هردو واگرا هستند.
ب) اگر
و 
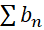همگرا باشد, آنگاه
نیز همگراست.
ج) اگر
و
واگرا باشد, آنگاه
واگراست.
سری های متناوب
آزمون سری های متناوب
فرض کنیم
یک دنبالهمثبت و غیرافزایشی باشد, یعنی به ازای هر
,
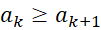باشد به صورتی که داشته باشیم
, در این صورت سری‌های متناوب زیر همگرا خواهند بود:
قضیه
فرض کنیم سری متناوب 
درشرایط آزمون سری متناوب صدق کند. در این صورت خطای حاصل از تقریب مجموع این سری همگرا با مجموع جزئی
ام آن کمتر از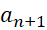
است.
همگرایی مطلق و مشروط
اگر سری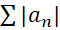 
همگرا باشد, می‌گوییم که سری
همگرای مطلق است.
اگر سری
همگرا باشد ولی
واگرا باشد( یعنی این سری همگرای مطلق نباشد ), آنگاه می‌گوییم که سری
همگرای مشروط است.
اگر سری
همگرای مطلق باشد, آنگاه همگراست و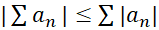
خواهد بود.
قضیه
فرض کنیم
یک سری باشد در این صورت خواهیمداشت:
الف) آزمون مقایسه:
اگر به ازای هر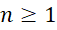
,
و 
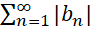همگرا باشد, آنگاه
همگرای مطلق است.
ب) آزمون مقایسه حدی:
اگر
و 
همگرا باشد, آنگاه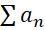
همگرای مطلق است.
آزمون نسبت
فرض کنیم جمله‌های سری
غیرصفر باشند, دراین صورت خواهیمداشت:
الف) اگر
آنگاه سری داده شده, همگرای مطلق است.
ب) اگر
یا
, در این صورت سری داده شده واگرا است.
پ) اگر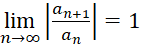
باشد, نتیجه‌ای در مورد همگرایی یا واگرایی این سری نمی‌توان به دست آورد. یعنی این سری می‌تواند همگرا یا واگرا باشد.
آزمون ریشه
فرض کنیم 
یک سری با جمله‌های ناصفر باشد. در این صورت خواهیمداشت:
الف) اگر
باشد, در این صورت سری داده شدههمگرای مطلق است.
ب) اگر
و یا
باشد, در این صورت سری داده شدهواگراست.
پ) اگر
باشد, هیچ نتیجه‌ای در مورد همگرایی یا واگرایی این سری به دست نمی‌آید. یعنی این سری می‌تواند همگرا و یا واگرا باشد.
- فرض کنید
یک دنباله باشد. اگر داشته‌باشیم
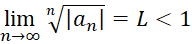و یا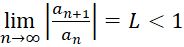 
آنگاه خواهیم داشت:
برای تسلط بیشتر بر این مباحث، می‌توانید کپسول آموزش ریاضی عمومی2 لینوم را هم مشاهده کنید.