سری های توانی

در اینآموزش ریاضی دولینوم، به سراغ یادگیری سریهای توانی میرویم.
یک سری به صورت را یک سری توانی به مرکز 0 میگوییم. اکنون اگر عدد
را یک سری توانی به مرکز 0 میگوییم. اکنون اگر عدد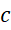 یک عدد حقیقی باشد, سری زیر را یکسری توانی به مرکز
یک عدد حقیقی باشد, سری زیر را یکسری توانی به مرکز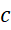 مینامیم.
مینامیم.
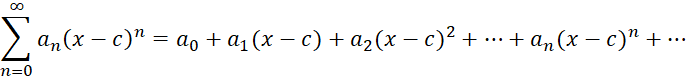
نکته: برای سادگی کار, حتی در زمانی که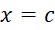 است, فرض میکنیم که
است, فرض میکنیم که
قضیه:
اگر سری توانی به ازای عدد ناصفر
به ازای عدد ناصفر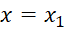 همگرا باشد, آنگاه به ازای هر مقدار از
همگرا باشد, آنگاه به ازای هر مقدار از که
که همگرا یا همگرای مطلق است.
همگرا یا همگرای مطلق است.
اگر سری توانی به ازای عدد ناصفر
به ازای عدد ناصفر همگرا باشد, آنگاه به ازای هر مقدار از
همگرا باشد, آنگاه به ازای هر مقدار از که
که واگراست.
واگراست.
قضیه:
اگر سری توانی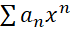 یک سری توانی باشد, آنگاه دقیقا یکی از حالتهای زیر رخ خواهد داد:
یک سری توانی باشد, آنگاه دقیقا یکی از حالتهای زیر رخ خواهد داد:
1) این سری تنها به ازای همگراست.
همگراست.
2) این سری به ازای هر مقدار همگرا یا همگرای مطلق است.
همگرا یا همگرای مطلق است.
3) عدد مثبت وجود دراد به طوری که سری فوق همگرای مطلق است اگر
وجود دراد به طوری که سری فوق همگرای مطلق است اگر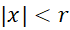 و واگراست اگر داشته باشیم
و واگراست اگر داشته باشیم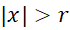 .
.
اگر به جای سری توانی , سری توانی
, سری توانی را درنظر بگیریم, آنگاه با قرار دادن
را درنظر بگیریم, آنگاه با قرار دادن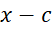 درحالتهای 1 و 3 قضیه قبل, این احکام به صورت زیر تبدیل میشوند:
درحالتهای 1 و 3 قضیه قبل, این احکام به صورت زیر تبدیل میشوند:
1) این سری تنها به ازای همگراست.
همگراست.
3) عدد مثبت وجود دراد به طوری که سری فوق همگرای مطلق است اگر
وجود دراد به طوری که سری فوق همگرای مطلق است اگر و واگراست اگر داشته باشیم
و واگراست اگر داشته باشیم .
.
تعریف:
عدد مذکور در قضیه قبل و در تذکر زیر آن را شعاع همگرایی سری توانی گوییم. اگر حالت 1 رخ دهد,
مذکور در قضیه قبل و در تذکر زیر آن را شعاع همگرایی سری توانی گوییم. اگر حالت 1 رخ دهد, و اگر حالت 2 صادق باشد, شعاع همگرایی را
و اگر حالت 2 صادق باشد, شعاع همگرایی را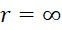 تعریف میکنیم. مجموعه همه مقادیر
تعریف میکنیم. مجموعه همه مقادیر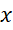 را که به ازای آنها سری توانی داده شده همگراست,بازه همگرایی آن سری میگوییم.
را که به ازای آنها سری توانی داده شده همگراست,بازه همگرایی آن سری میگوییم.
مشتق گیری و انتگرال گیری از سریهای توانی
قضیه مشتق گیری سریهای توانی:
اگر یک سری توانی با شعاع همگرایی
یک سری توانی با شعاع همگرایی باشد آنگاه خواهیم داشت:
باشد آنگاه خواهیم داشت:
الف) شعاع همگرایی سری , که حاصل از مشتقگیری جمله به جمله سری داده شده است, برابر
, که حاصل از مشتقگیری جمله به جمله سری داده شده است, برابر است.
است.
ب) به ازای هر مقدار در بازه
در بازه خواهیم داشت:
خواهیم داشت:

اگر چه قضیه مشتقگیری سریهای توانی بیان میکند که شعاعهای همگرایی دو سری توانی و
و یکسان هستند, ولی نمیتوان نتیجه گرفت که بازههای همگرایی آنها نیز یکی است. به عنوان مثال بازه همگرایی
یکسان هستند, ولی نمیتوان نتیجه گرفت که بازههای همگرایی آنها نیز یکی است. به عنوان مثال بازه همگرایی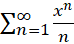 برابر است با
برابر است با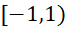 درحالی که بازه همگرایی سری مشتق آن یعنی
درحالی که بازه همگرایی سری مشتق آن یعنی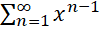 برابر است با
برابر است با .
.
تذکر
اگرچه قضیه مشتقگیری بیان میکند که مشتق سری توانی , با شعاع همگرایی ناصفر, وجود دارد ولی چون سری مشتق شده خود یک سری توانی با همان شعاع همگرایی است, از این سری نیز میتوان مشتق گرفت و درنتیجه سری داده شده دوبار مشتق پذیر است. با تکرار این روند نتیجه میگیریم که همه مشتقهای یکسری توانی با شعاع همگرایی
, با شعاع همگرایی ناصفر, وجود دارد ولی چون سری مشتق شده خود یک سری توانی با همان شعاع همگرایی است, از این سری نیز میتوان مشتق گرفت و درنتیجه سری داده شده دوبار مشتق پذیر است. با تکرار این روند نتیجه میگیریم که همه مشتقهای یکسری توانی با شعاع همگرایی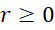 در بازه
در بازه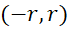 وجود دارند.
وجود دارند.
قضیه انتگرال گیری سریهای توانی

اگر شعاع همگرایی سری توانی برابر
برابر باشد, آنگاه خواهیم داشت:
باشد, آنگاه خواهیم داشت:
1) شعاع همگرایی سری , حاصل از انتگرالگیری جمله به جمله از سری یاد شده برابر با
, حاصل از انتگرالگیری جمله به جمله از سری یاد شده برابر با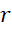 است.
است.
2) به ازای هرمقدار در بازه
در بازه داریم:
داریم:

سری تیلور
اگر بتوان تابع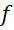 را به صورت سری
را به صورت سری نمایش داد, به این نمایش, نمایشسری مک لورن تابع
نمایش داد, به این نمایش, نمایشسری مک لورن تابع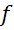 میگویند.
میگویند.
اگر بتوان تابع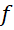 را به صورت سری
را به صورت سری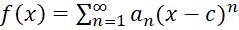 نمایش داد, به این نمایش, نمایشسری تیلور تابع
نمایش داد, به این نمایش, نمایشسری تیلور تابع میگویند.
میگویند.
قضیه
همه مشتقهای دربازه بازی شامل
دربازه بازی شامل چون
چون وجود داشته باشند, انگاه این توابع را میتوان به ازای مقادیر
وجود داشته باشند, انگاه این توابع را میتوان به ازای مقادیر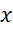 در
در توسط سری تیلور
توسط سری تیلور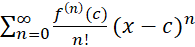 نمایش داد اگر و فقط اگر داشته باشیم:
نمایش داد اگر و فقط اگر داشته باشیم:
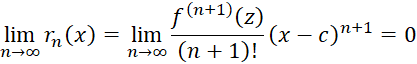
در این عبارت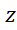 عددی بین
عددی بین و
و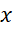 است.
است.
سری دوجمله ای
اگر یک عددحقیقی باشد, آنگاه اگر
یک عددحقیقی باشد, آنگاه اگر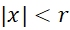 باشد خواهیم داشت:
باشد خواهیم داشت:
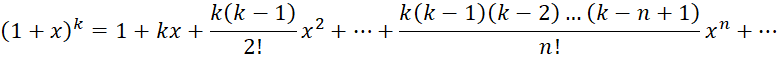

نکته:
چون سری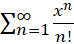 به ازای هر
به ازای هر همگراست, پس به ازای هر
همگراست, پس به ازای هر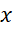 ,
,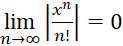 به این ترتیب چون سری
به این ترتیب چون سری به ازای هر
به ازای هر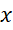 همگراست, پس به ازای هر
همگراست, پس به ازای هر ,
,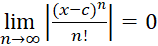 خواهد بود.
خواهد بود.
برای تسلط بیشتر بر این مباحث، میتوانید کپسول آموزش ریاضی عمومی2 لینوم را هم مشاهده کنید.