استفاده از قضایای مربوط به تبدیل لاپلاس

این روش نیز پیش از این بیان و استفاده شده است.

 

حل معادلات با استفاده از لاپلاس

یکی از کاربرد هایلاپلاس در حل معادلات دیفرانسیلی و انتگرالی می باشد که در ادامه به آن ها خواهیم پرداخت.

معادله انتگرالی

تعریف

معادله انتگرالیمعادله ای است که در آن تابع مجهول زیر انتگرال واقع می شود و فرم کلی آن به صورت زیر است:

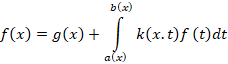
تابع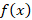 تابع مجهولی است که باید آن را بیابیم.

توجه: برای حل معادلات دیفرانسیلی و انتگرالی عبارت زیر را به خاطر داشته باشید:

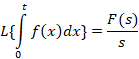
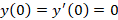مثال: اگر داشته باشیم معادله زیر را حل کنید.

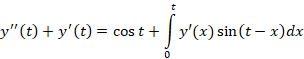
ابتدا از طرفین معادله لاپلاس می گیریم:

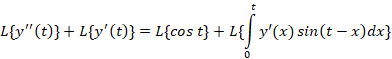
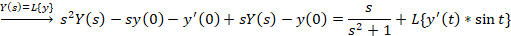
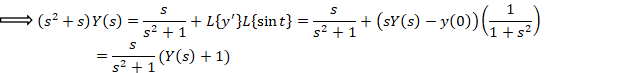
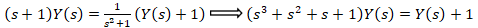
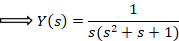
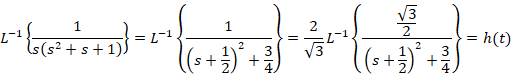
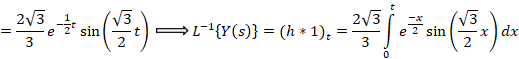
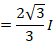
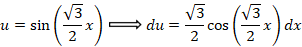
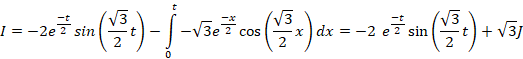
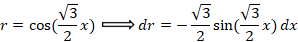
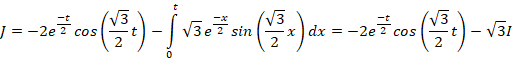
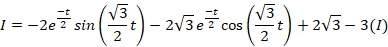
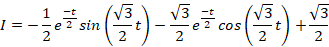
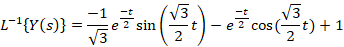
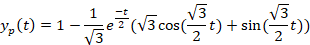
مثال: با فرض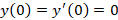 معادله  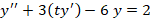را حل کنید.

از طرفین معادله لاپلاس می گیریم:

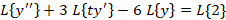
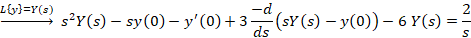
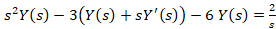
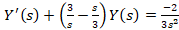
به یک معادله دیفرانسیل خطی مرتبه اول رسیدیم که با حل آن به عبارت زیر خواهید رسید:

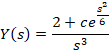
برای وارون گرفتن از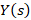 باید ثابت 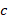را مشخص کنیم:

دستگاه معادلات دیفرانسیل

برای حل دستگاهمعادلات دیفرانسیل روش های متفاوتی وجود دارد که عبارتند از:

1-روش حذفی

2-روش تبدیل لاپلاس

3-روش ماتریسی یا مقادیر ویژه

ما در ادامه به بررسی هر یک از موارد فوق به تفکیک خواهیم پرداخت.

روش حذفی

احتمالا با حل دستگاه به روش حذفی پیش از این آشنایی دارید ، برای درک بهتر آن به حل مثال زیر توجه فرمایید.

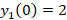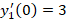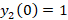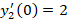مثال: اگر داشته باشیم ، ، و دستگاه معادله دیفرانسیل زیر را با روش حذفی حل کنید.

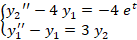
از معادله ی دوم مشتق گرفته و در معادله اول قرار می دهیم:

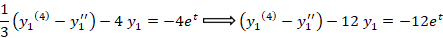
معادله مشخصه معادله را مشخص می کنیم تا جواب عمومی آن را بدست آوریم:

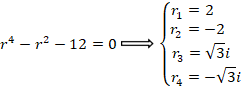
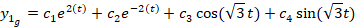
جواب خصوصی معادله به صورت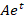 است که با جایگذاری در معادله مقدار 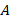یک بدست خواهد آمد و داریم:

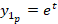
و جواب عمومی نیز به صورت زیر بدست خواهد آمد:

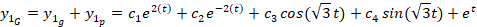
با توجه به معادله دوم:

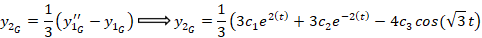
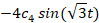
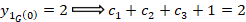
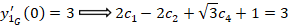
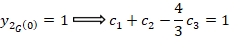
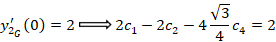
در نتیجه مقادیر زیر بدست می آید:

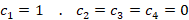
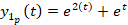
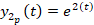
روش تبدیل لاپلاس

در این روش از طرفین تمام معادلات لاپلاس می گیریم سپس با استفاده از روش کرامر جواب دستگاه حاصل را بدست می آوریم و در نهایت با استفاده از لاپلاس معکوس به جواب دستگاه اولیه خواهیم رسید.

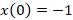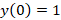مثال: با توجه به این که و  دستگاه معادلات زیر را به روش لاپلاس حل کنید.

 

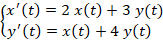
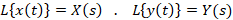
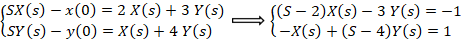
دستگاه را با روش کرامر حل می کنیم:

 

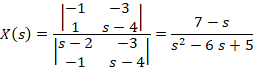
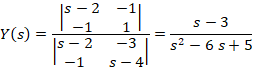
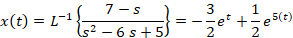
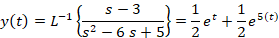
روش ماتریسی یا مقادیر ویژه

برای حل دستگاه به روش ماتریسی ابتدا باید با دو مفهوم مقدار ویژه و بردار ویژه آشنا گردید.

مقدار ویژه

ریشه های چندجمله ای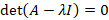 را مقادیر ویژه ماتریس 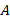می گوییم.

بردار ویژه

بردار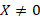 را بردار ویژه ی متناظر با مقدار ویژه ی 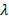گوییم هر گاه:

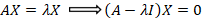
مثال: مقادیر ویژه و بردارهای ویژه ماتریس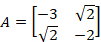 را بدست آورید.

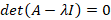
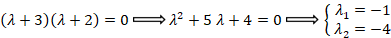
حل دستگاه معادلات دیفرانسیل خطی مرتبه اول با ضرایب ثابت

اگر یک دستگاه به صورت زیر داشته باشیم:

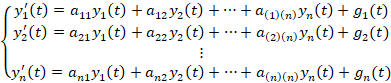
آنگاه داریم:

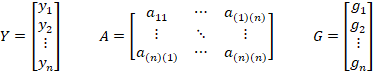
و جواب عمومی دستگاه به فرم زیر است:

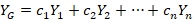
که در این رابطه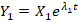 و به همین ترتیب ادامه می یابد تا نهایتا.

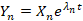توجه

به ازای هر بردار دلخواه ، 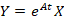جواب دستگاه 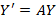است . اگر نتوانیم یک بردار ویژه مستقل خطی با 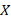، متناظر با 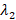بیابیم برای 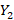مستقل از 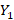داریم :

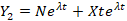
به همین ترتیب اگر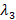 نیز با 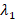و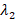 برابر باشد و نتوانیم بردار ویژه ی مستقل خطی با 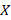بیابیم ، برای 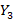متسقل از 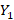و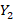 داریم:

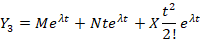
و به همین ترتیب ادامه پیدا می کند.

مثال: دستگاه زیر را حل کنید.

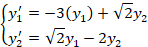
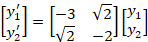
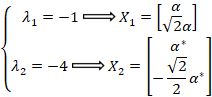
باید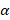α وα*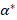 را به گونه ای قرار دهیم که 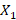و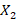 مستقل خطی شوند:

 

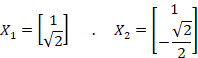
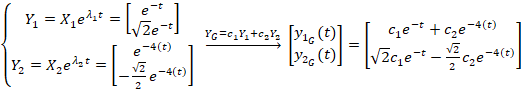
مثال: دستگاه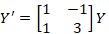 زیر را حل کنید.

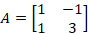
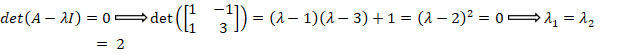
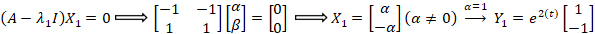
دو بردار ویژه مستقل ندارد:

---

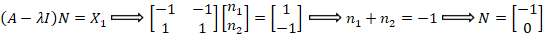
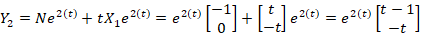
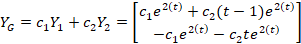
برای تسلط بیشتر بر این مباحث، می‌توانید  کپسول آموزشی معادلات دیفرانسیللینوم را  مشاهده کنید.