8) حل معادلات دیفرانسیل بامشتقات جزئی مرتبه دوم
در اینآموزش کپسولی لینوم، به سراغ معادلات دیفرانسیل مشتق جزئی میرویم.
در درسمعادلاتدیفرانسیل با حل مسائل متنوعی از معادلاتدیفرانسیل آشنا شدیم. همانطورکه میدانید یک معادله دیفرانسیل عبارت است از : 
با تابعی از
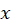که یک معادله را تشکیل میدهد. منظور از حل یک معادله دیفرانسیل یافتن تابع
است. مثلا یک معادله دیفرانسیل به صورت زیر است:
یادآوری1-یک معادله دیفرانسیل خطی مرتبه اول به صورت زیر است:
همانطور که میدانید جواب معادله فوق به صورت زیر قابل محاسبه است:
یادآوری2-یکمعادله دیفرانسیل خطی مرتبه دوم با ضرایب ثابت همگن به صورت زیر است:
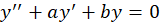
مثال1 )جواب معادلات زیر را بیابید.
حل:
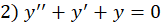
حل:
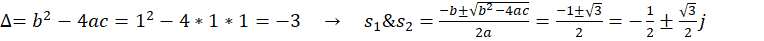
1-8 تعریف معادله دیفرانسیل مرتبه دوم با مشتقات جزئی
در یک معادله دیفرانسیل تابع
تابعی فقط از یک متغییر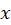 
است.
در بحثمعادلات دیفرانسیل با مشتقات جزئی یک تابع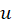
تابعی از چندین متغییر است: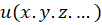
در این فصل معادلاتی را بررسی میکنیم که در آنها تابع شامل 2 متغییر است.
نمونههای زیادی از این معادلات در کاربردهای مهندسی وجود دارد، مثل: معادله یک نخ مرتعش که بهمعادله موجمعروف است یا مسئله گرم شدن که بهمعادله گرما معروف است یا حل معادله پتانسیل الکتریکی در یک فضای دوبعدی که بهمعادله لاپلاسمعروف است.
تعریف یک معادله دیفرانسیل با مشتقات جزئی
یک معادله دیفرانسیل با مشتقات جزئی در حالت کلی به صورت زیر تعریف میشود:
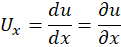
موارد زیر نمونههایی از معادلات دیفرانسیل با مشتقات جزئی هستند:
تعریف مرتبه یک معادله دیفرانسیل با مشتقات جزئی
به بالاترین درجه مشتقگیری در یک معادله با مشتقات جزئی مرتبه آن معادله گوییم.
تعریف معادله دیفرانسیل با مشتقات جزئی خطی
معادله دیفرانسیلی با مشتقات جزئی را خطی نامیم اگر این معادله نسبت به
و همه مشتقات آن خطی باشد.
نکته-هر عملی جز ضرب کردن، معادله را غیرخطی میکند.
یک معادله دیفرانسیل با مشتقات جزئیخطی مرتبه دومبا دو متغییر مستقل دارای شکل زیر است:
که در آن ضرایب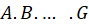 
توابعی از
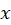و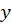
میباشند. اگر معادله به شکل بالا نباشد، آن راغیرخطیمینامیم.
یکمعادله خطی راهمگننامیم اگر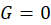 
باشد، در غیر اینصورت آن را ناهمگننامیم.
2-8 انواع معادلات دیفرانسیل با مشتقات جزئی مرتبه دوم
میتوان این معادلات را بر حسب مقدار
به 3 دسته زیر تقسیمبندی کرد:
1)معادلات دیفرانسیل با مشتقات جزئی مرتبه دومهذلولیگون:
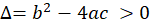
2)معادلات دیفرانسیل با مشتقات جزئی مرتبه دومسهمیگون:
3)معادلات دیفرانسیل با مشتقات جزئی مرتبه دومبیضیگون:
از مهمترین معادلات با مشتقات جزئی میتوان به معادلات زیر اشاره کرد:
معادله انتقال گرما (سهموی)
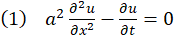
معادله انتشار موج (هذلولوی)
معادله پتانسیل (بیضوی)
3-8 روشهای حل معادلات دیفرانسیل با مشتقات جزئی مرتبه دوم
هدف از حل معادله دیفرانسیل با مشتقات جزئی محاسبه تابع
است که در این معادله صدق کند.
چهار روش مهم برای حل این معادلات عبارتند از :
الف) روش فاکتورگیری : این روش هنگامی امکانپذیر است که بتوان در معادله از یکی از عبارات 
یا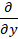 
فاکتورگیری نمود.
ب) روش تغییرمتغییر: معادله کلی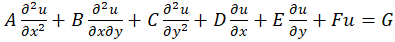
را در نظرمیگیریم. برای حل این مسئله به کمک روش تغییرمتغییر معادله مشخصه زیر را تشکیل میدهیم.
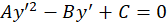
معادله مشخصه بر حسب 
سه حالت زیر را خواهدداشت.
الف)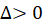 
: تغییرمتغییر به
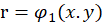و
ب)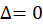 
: تغییرمتغییر به
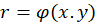و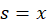 
ج)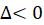 
: نمیتوان در این حالت از روش تغییرمتغییر معادله را حل نمود. در صورتی که بتوان
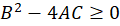را تشکیل دهیم میتوان از روش تغییرمتغییر معادله را حل نمود.
ج) روش ضربی (جداسازی متغییرها):این روش یکی از روشهای مهم برای حل معادله دیفرانسیل با مشتقات جزئی میباشد. سه معادله مهم موج، گرما و لاپلاس از این روش قابل حل هستند. در این روش تابع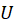
که شامل دو متغییر مستقل است ( مثلا 
یا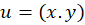 
) به عنوان تابعی از حاصلضرب توابعی از متغییرهای مستقل تعریف نمود. یعنی:
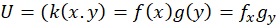
**شرط استفاده از روش ضربی: حال تابع را در معادله جایگذاری میکنیم. اگر بتوان تمام توابع وابسته به را به یک طرف تساوی و تمام توابع را به طرف دیگر تساوی انتقال داد آن وقت این معادله از روش ضربی قابل حل خواهدبود.
د) روش دالامبر: این روش فقط برای حل معادله موج به صورت 
بهکارمیرود.
مثال2 )معادله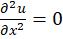
را حل کنید.
حل:با توجه به چهار روش ذکرشده میتوان از روش فاکتورگیری استفاده نمود. در نتیجه داریم:
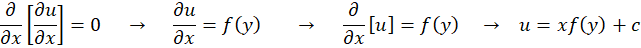
مثال3 )معادله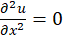
را حل کنید.
حل:با توجه به چهار روش ذکرشده میتوان از روش فاکتورگیری استفاده نمود. در نتیجه داریم:
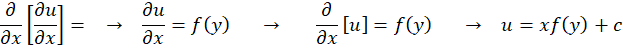
مثال4 )معادله
را حل کنیدو جواب عمومی آن را بهدستآورید.
حل:با توجه به روشهای ذکرشده میبایست از روش تغییرمتغییر استفاده نمود:
حال میبایست معادله اصلی را که متغییرهای آن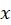
و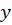
هستند به معادلهای تبدیل کنیم که متغییرهای آن 
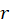و
اند. برای این امر باید عبارات زیر را محاسبه کنیم:
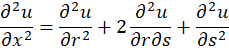
حال عبارت دارای
و 
را در معادله اصلی قرارمیدهیم:
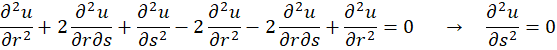
حال این معادله به روش فاکتورگیری قابل حل است:
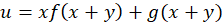
4-8 حل معادله موج
اگر نخ قابل ارتعاشی از یک طرف به مانع محکمی یا از دو طرف به این مانع متصل شود و این نخ با استفاده از نیروی اولیهای شروع به ارتعاش نماید، معادلهای برای این نخ مرتعش حاکم است که بهمعادله موجمعروف است.
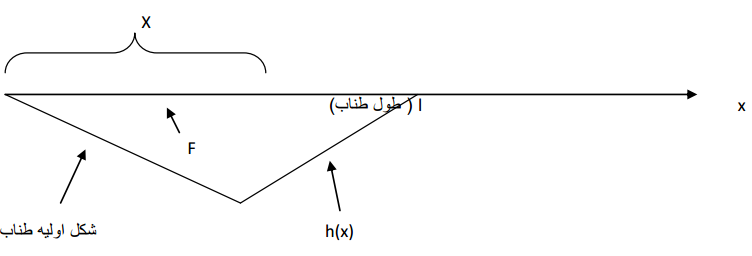
اگر در هر نقطه در فاصله صفر تا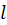
به این نخ نگاه کنیم در هرلحظه از زمان این نخ ارتفاع خاصی خواهدداشت
اثبات شدهاستکه معادله دیفرانسیل متناظر با این حرکت ارتعاشی به صورت زیر است:
هدف، حل این معادله دیفرانسیل با مشتقات جزئی است. یعنی محاسبه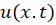
. با توجه به صورت مسئله داریم:
شرایط اولیه: الف) 
ب)
شرایط مرزی: الف)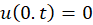 
ب)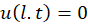 
وقتی این معادله دیفرانسیل با مشتقات جزئی،حل شود جواب آن به صورت زیر است:
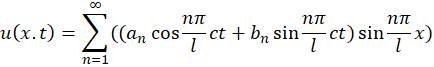
و در حالت خاص اگر در لحظه اولیه سرعت طناب صفر باشد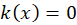 
و 
خواهیم داشت:
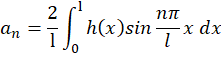
مثال5 )با استفاده از جواب معادله موج معادلات حرکت طنابی مرتعش را بهدستآورید که سرعت اولیه آن صفر است و شکل آن در لحظه ارتعاش به صوت زیر است و سرعت موج یک است.
حل:طبق صورت سوال داریم: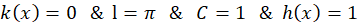 
با توجه به اینکه سرعت اولیه صفر میباشد فقط کافی است ضریب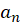
محاسبه شود.
5-8 حل معادله گرما ( انتقال حرارت)
فرض کنیم میلهای با طول محدود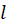
از یک طرف حرارت دادهشود. میخواهیم مقدار حرارت را در هر نقطه و در هر زمان بهدستآوریم. در فیزیک حرارت معادله دیفرانسیل متناظر با این مسئله به صورت زیر بهدستمیآید.
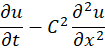
هدف، حل این معادله است. یعنی محاسبه
. با توجه به صورت مسئله داریم:
شرایط اولیه: الف)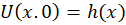 
شرایط مرزی: الف)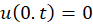 
ب)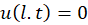 
وقتی این معادله دیفرانسیل با مشتقات جزئی، حل شود جواب آن به صورت زیر است:
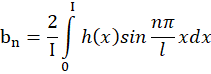
مثال6 )جواب معادله گرما به صورت 
و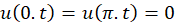 
با پارامتر 
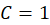را بهدستآورید.
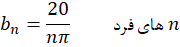
6-8 حلمعادله لاپلاس
معادله دیفرانسیل متناظر با این مسئله به صورت زیر بهدستمیآید:
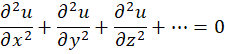
در فضای دوبعدی به صورت خاص 
قابل بیان است. کاربرد این معادله در محاسبه اختلاف پتانسیل به وجودآمده در سطوح رسانا میباشد. این معادله با استفاده از روش ضربی قابل حل است: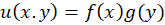 
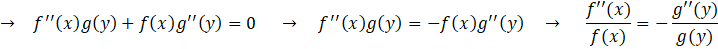
دریافتیم که این معادله دیفرانسیل با مشتقات جزئی، با روش ضربی قابل حل است:
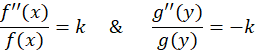
الف)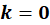 
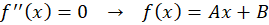
ب)
ج)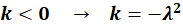
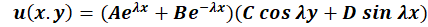
همان طور که میبینید این معادله نیز دارایهس جواب است که جواب خصوصی معادله با استفاده از اعمال شرایط اولیه و مرزی محاسبه خواهدشد.
7-8 روش دالامبر
این روش فقط برای حل معادله موج به صورت:
به کار میرود که در این معادله شرایط اولیه و مرزی به صورت زیر هستند:
شرایط اولیه: الف)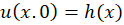
ب) 
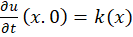
شرایط مرزی: الف) 
ب)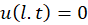 
وقتی معادلات مربوطه حل شود، در نهایت جواب دالامبر معادله موج عبارت است از:
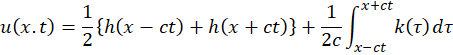
مثال 7)فرض کنید نخ در لحظه صفر دارای سرعت اولیه صفر است و شکل طناب در لحظه اول به صورت زیر است، اگر پارامتر سرعت موج 1 باشد، معادله حرکت نخ را به روش دالامبر در هر لحظه از زمان بیابید.
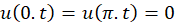
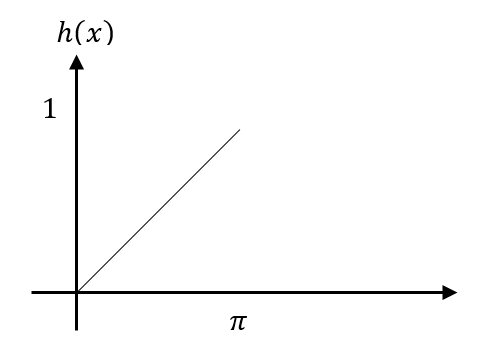
ابتدابایستی مقدار را محاسبه کنیمکه از محاسبه شیب خط داریم: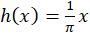 
. در این مسئله سرعت اولیه صفر است یا به عبارتی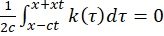
از طرفی میدانیم که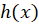
را میتوان یک تابع متناوب فرد با دوره تناوب
در نظرگرفت و سری فوریه آن به شرح زیر است:
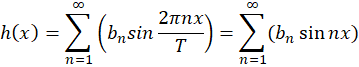
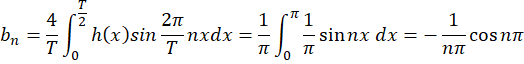
برای تسلط بیشتر بر این مباحث، میتوانید کپسول آموزشی معادلات دیفرانسیل لینوم را هم مشاهده کنید.